
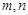 是两条不同的直线,
是两条不同的直线,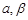 是两个不同的平面,下列命题正确的( )
是两个不同的平面,下列命题正确的( )A.若 则 则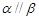 |
B.若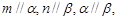 则 则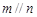 |
C.若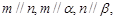 则 则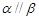 |
D.若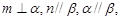 则 则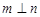 |
科目:高中数学 来源:不详 题型:填空题
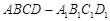 的表面上有一动点P由顶点A出发按下列规则向点
的表面上有一动点P由顶点A出发按下列规则向点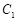 移动:①点P只能沿正方体木块的棱或表面对角线移动;②点P每一变化位置,都使P点到点
移动:①点P只能沿正方体木块的棱或表面对角线移动;②点P每一变化位置,都使P点到点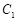 的距离缩短,③若在面对角线上移动时,不能在中点处转入另一条面对角线,动点P共有_______种不同的运行路线.
的距离缩短,③若在面对角线上移动时,不能在中点处转入另一条面对角线,动点P共有_______种不同的运行路线.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.若l平行于α,则l平行于α内的所有直线 |
B.若m α,l α,l β,且m∥l,则α∥β β,且m∥l,则α∥β |
C.若m α,l α,l β,且m⊥l,则α⊥β β,且m⊥l,则α⊥β |
D.若m β,m⊥α,则α⊥β β,m⊥α,则α⊥β |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
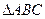 中∠ACB=90°,AS=BC=1,AC=2,SA⊥面ABC,AD⊥SC于D,
中∠ACB=90°,AS=BC=1,AC=2,SA⊥面ABC,AD⊥SC于D,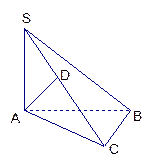
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
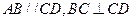 ,侧面SAB为等边三角形,
,侧面SAB为等边三角形,
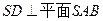 ;
; 求AB与平面SBC所成的角的大小。
求AB与平面SBC所成的角的大小。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 中,AB=AD=1,AA1=2,M是棱CC1的中点
中,AB=AD=1,AA1=2,M是棱CC1的中点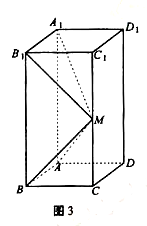
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com