
19(本小题满分13分)
随机抽取某中学甲乙两班各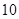 名同学,测量他们的身高(单位:
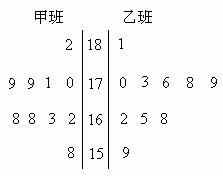
名同学,测量他们的身高(单位: 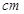 ),获得身高数据的茎叶图如下图:
),获得身高数据的茎叶图如下图:
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
 (3)现从乙班这
(3)现从乙班这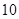 名同学中随机抽取两名身高不低于
名同学中随机抽取两名身高不低于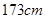 的同学,求身高为
的同学,求身高为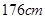 的同学被抽中的概率。
的同学被抽中的概率。
解:(1)由茎叶图可知:甲班身高集中于160~179之间,而乙班身高集中于170~180之间。因此乙班平均身高高于甲班。……………………………4分
(2) 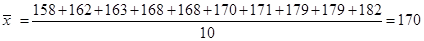 ……6分
……6分
甲班的样本方差为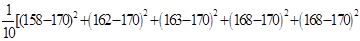
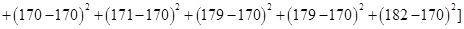 =57.2
=57.2
…………10分
(3)设身高为176cm的同学被抽中的事件为A。
从乙班10名同学中抽中两名身高不低于173cm的同学有:(181,173) (181,176)
(181,178) (181,179) (179,173) (179,176) (179,178) (178,173)
(178, 176) (176,173)共10个基本事件,而事件A含有4个基本事件;(12分)
 …………………13分
…………………13分
【解析】略


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
(08年广东卷文)(本小题满分13分)
某初级中学共有学生2000名,各年级男、女生人数如下表:
| 初一年级 | 初二年级 | 初三年级 |
女生 | 373 | x | y |
男生 | 377 | 370 | z |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1) 求x的值;
(2) 现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
(3) 已知y![]() 245,z
245,z![]() 245,求初三年级中女生比男生多的概率.
245,求初三年级中女生比男生多的概率.
查看答案和解析>>
科目:高中数学 来源:2008年普通高等学校招生全国统一考试理科数学(重庆卷) 题型:解答题
(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分.)
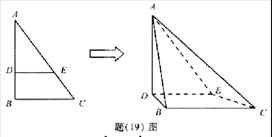
如题(19)图,在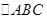 中,B=
中,B=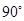 ,AC=
,AC=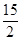 ,D、E两点分别在AB、AC上。使
,D、E两点分别在AB、AC上。使
 ,DE=3。现将
,DE=3。现将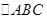 沿DE折成直二角角,求:
沿DE折成直二角角,求:
(Ⅰ)异面直线AD与BC的距离;
(Ⅱ)二面角A-EC-B的大小(用反三角函数表示)。
查看答案和解析>>
科目:高中数学 来源: 题型:
(2012年高考福建卷理科19)(本小题满分13分)
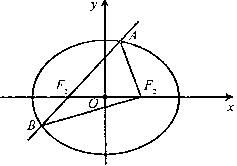 如图,椭圆
如图,椭圆![]() 的左焦点为
的左焦点为![]() ,右焦点为
,右焦点为![]() ,离心率
,离心率![]() 。过
。过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,且
两点,且![]() 的周长为8。
的周长为8。
(Ⅰ)求椭圆![]() 的方程。
的方程。
(Ⅱ)设动直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点
有且只有一个公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() 。试探究:
。试探究:
在坐标平面内是否存在定点![]() ,使得以
,使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,说明理由。
的坐标;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
(2010湖南理数)19.(本小题满分13分)
为了考察冰川的融化状况,一支科考队在某冰川上相距8km的A,B两点各建一个考察基地。视冰川面为平面形,以过A,B两点的直线为x轴,线段AB的的垂直平分线为y轴建立平面直角坐标系(图6)在直线x=2的右侧,考察范围为到点B的距离不超过![]() km区域;在直线x=2的左侧,考察范围为到A,B两点的距离之和不超过
km区域;在直线x=2的左侧,考察范围为到A,B两点的距离之和不超过![]() km区域。
km区域。
(Ⅰ)求考察区域边界曲线的方程;
(Ⅱ)如图6所示,设线段P1P2,P2P3是冰川的部分边界线(不考虑其他边界线),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km,以后每年移动的距离为前一年的2倍,求冰川边界线移动到考察区域所需的最短时间。


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com