
用数学归纳法证明:

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
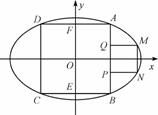
如图,正方形ABCD内接于椭圆 =1(a>b>0),且它的四条边与坐标轴平行,正方形MNPQ的顶点M、N在椭圆上,顶点P、Q在正方形的边AB上,且A、M都在第一象限.
=1(a>b>0),且它的四条边与坐标轴平行,正方形MNPQ的顶点M、N在椭圆上,顶点P、Q在正方形的边AB上,且A、M都在第一象限.
(1) 若正方形ABCD的边长为4,且与y轴交于E、F两点,正方形MNPQ的边长为2.
① 求证:直线AM与△ABE的外接圆相切;
② 求椭圆的标准方程;
(2) 设椭圆的离心率为e,直线AM的斜率为k,求证:2e2-k是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面几何里可以得出正确结论:“正三角形的内切圆半径等于这正三角形的高的 ”.拓展到空间,类比平面几何的上述结论,则正四面体的内切球半径等于这个正四面体的高的________ .
”.拓展到空间,类比平面几何的上述结论,则正四面体的内切球半径等于这个正四面体的高的________ .
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{bn}是等差数列,b1=1,b1+b2+…+b10=145.
(1) 求数列{bn}的通项公式bn;
(2) 设数列{an}的通项an=loga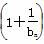 (其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与
(其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与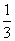 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
用数学归纳法证明“12+22+32+…+n2= n(n+1)(2n+1)(n∈N*)”,当n=k+1时,应在n=k时的等式左边添加的项是________.
n(n+1)(2n+1)(n∈N*)”,当n=k+1时,应在n=k时的等式左边添加的项是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com