Question

如下图,A村在B地正北 km处,C村在B地正东4 km处,已知弧形公路PQ上任一点到B、C两点的距离之和为8 km,现要在公路旁建造一个交电房M分别向A村、C村送电,但C村有一村办工厂用电需用专用线路,不得与民用混线用电,因此向C村要架两条线路分别给村民和工厂送电,要使用电线最短,电房M应建在A村的什么方位,并求出M到A村的距离.

Answer 1

思路分析：要把实际问题转化成数学问题，首先要建立适当的直角坐标系，然后利用椭圆的第一和第二定义解答.

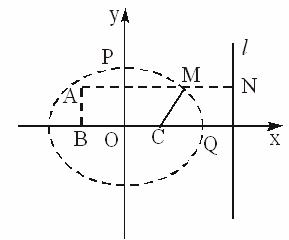
解：以直线BC为x轴,线段BC的中垂线为y轴,建立如图所示的直角坐标系,由题意得|MB|+|MC|=8＞4=|BC|.

∴点M在以B、C为焦点,长轴长为8 km的椭圆上.

由2a=8,2c=4,得a=4,c=2,b=.

∴椭圆方程为=1.

其中准线l：x=8,离心率e=,

作MN⊥l于N,

则=,|MN|=2|MC|.

作AE⊥l于E交椭圆于M′(M′介于A、E之间).

∴|MA|+2|MC|=|MA|+|MN|≥|M′A|+|M′E|=|AE|=8-(-2)=10.

∴(|MA|+2|MC|)_min=10,此时M与M′的点重合.

由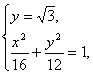y=3,

解得M′(),

即M().

此时|AM|=+2=2(+1).

答：要使所用电线最短,电房M应建在A的正东方向,距A村2(+1) km处.