
分析 首项根据等差数列的性质Sm,S2m-Sm,S3m-S2m仍然成等差数列,可得S10,S20-S10,S30-S20仍然成等差数列.进而代入数值可得答案.
解答 解:若数列{an}为等差数列则Sm,S2m-Sm,S3m-S2m仍然成等差数列.
所以S10,S20-S10,S30-S20仍然成等差数列.
所以2(S20-S10)=S10+S30-S20,
因为在等差数列{an}中有S10=4,S20=20,
2(20-4)=4+S30-20,
所以S30=48.
故答案为48.
点评 本题考查等差数列的性质,解决此类问题的关键是熟悉等差数列的前n项和的有关性质,此类题目一般以选择题或填空题的形式出现.


科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,$\frac{1}{3}$) | C. | [$\frac{1}{7}$,$\frac{1}{3}$) | D. | [$\frac{1}{7}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{8}$ |
查看答案和解析>>
科目:高中数学 来源:2017届江西吉安一中高三上学期段考一数学(文)试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
在平面直角坐标中,以坐标原点为极点,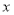 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线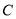 的极坐标方程为
的极坐标方程为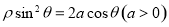 ,过点
,过点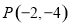 的直线
的直线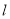 的参数方程为
的参数方程为 (
(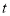 为参数),直线
为参数),直线 与曲线
与曲线 相交于
相交于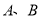 两点.
两点.
(1)写出曲线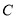 的直角坐标方程和直线
的直角坐标方程和直线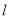 的普通方程;
的普通方程;
(2)若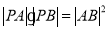 ,求
,求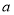 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2017届江西吉安一中高三上学期段考一数学(理)试卷(解析版) 题型:选择题
已知变量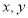 满足条件
满足条件 ,若目标函数
,若目标函数 仅在点
仅在点 处取得最大值,则
处取得最大值,则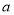 的取值范围是( )
的取值范围是( )
A.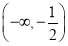 B.
B.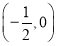 C.
C. D.
D.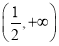
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com