设fk(n)为关于n的k(k∈N)次多项式.数列{an}的首项a1=1,前n项和为Sn.对于任意的正整数n,an+Sn=fk(n)都成立.
(I)若k=0,求证:数列{an}是等比数列;
(Ⅱ)试确定所有的自然数k,使得数列{an}能成等差数列.
【答案】
分析:(Ⅰ)若k=0,不妨设f
(n)=c(c为常数).即a
n+S
n=c,结合数列中a
n与 S
n关系
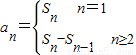
求出数列{a
n}的通项公式后再证明.
(Ⅱ)由特殊到一般,实质上是由已知a
n+S
n=f
k(n) 考查数列通项公式求解,以及等差数列的判定.
解答:(Ⅰ)证明:若k=0,则f
k(n)即f
(n)为常数,
不妨设f
(n)=c(c为常数).
因为a
n+S
n=f
k(n)恒成立,所以a
1+S
1=c,c=2a
1=2.
而且当n≥2时,
a
n+S
n=2,①
a
n-1+S
n-1=2,②
①-②得 2a
n-a
n-1=0(n∈N,n≥2).
若a
n=0,则a
n-1=0,…,a
1=0,与已知矛盾,所以a
n≠0(n∈N
*).
故数列{a
n}是首项为1,公比为

的等比数列.
(Ⅱ)解:(1)若k=0,由(Ⅰ)知,不符题意,舍去.
(2)若k=1,设f
1(n)=bn+c(b,c为常数),
当n≥2时,a
n+S
n=bn+c,③
a
n-1+S
n-1=b(n-1)+c,④
③-④得 2a
n-a
n-1=b(n∈N,n≥2).
要使数列{a
n}是公差为d(d为常数)的等差数列,
必须有a
n=b-d(常数),
而a
1=1,故{a
n}只能是常数数列,通项公式为a
n=1(n∈N
*),
故当k=1时,数列{a
n}能成等差数列,其通项公式为a
n=1(n∈N
*),
此时f
1(n)=n+1.
(3)若k=2,设f
2(n)=pn
2+qn+t(a≠0,a,b,c是常数),
当n≥2时,
a
n+S
n=pn
2+qn+t,⑤
a
n-1+S
n-1=p(n-1)
2+q(n-1)+t,⑥
⑤-⑥得 2a
n-a
n-1=2pn+q-p(n∈N,n≥2),
要使数列{a
n}是公差为d(d为常数)的等差数列,
必须有a
n=2pn+q-p-d,且d=2p,
考虑到a
1=1,所以a
n=1+(n-1)•2p=2pn-2p+1(n∈N
*).
故当k=2时,数列{a
n}能成等差数列,
其通项公式为a
n=2pn-2p+1(n∈N
*),
此时f
2(n)=an
2+(a+1)n+1-2a(a为非零常数).
(4)当k≥3时,若数列{a
n}能成等差数列,根据等差数列通项公式可知Sn是关于n的二次型函数,
则a
n+S
n的表达式中n的最高次数为2,
故数列{a
n}不能成等差数列.
综上得,当且仅当k=1或2时,数列{a
n}能成等差数列.
点评:本题考查数列通项公式的求解,等差数列的判定,考查阅读理解、计算论证等能力.

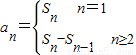 求出数列{an}的通项公式后再证明.
求出数列{an}的通项公式后再证明. 的等比数列.
的等比数列.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案