
【题目】已知函数![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)设![]() ,若
,若![]() ,均
,均![]() ,使得
,使得![]() ,求
,求![]() 的取值范围.
的取值范围.
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】某农业合作社生产了一种绿色蔬菜共![]() 吨,如果在市场上直接销售,每吨可获利
吨,如果在市场上直接销售,每吨可获利![]() 万元;如果进行精加工后销售,每吨可获利
万元;如果进行精加工后销售,每吨可获利![]() 万元,但需另外支付一定的加工费,总的加工
万元,但需另外支付一定的加工费,总的加工![]() (万元)与精加工的蔬菜量
(万元)与精加工的蔬菜量![]() (吨)有如下关系:
(吨)有如下关系: 设该农业合作社将
设该农业合作社将![]() (吨)蔬菜进行精加工后销售,其余在市场上直接销售,所得总利润(扣除加工费)为
(吨)蔬菜进行精加工后销售,其余在市场上直接销售,所得总利润(扣除加工费)为![]() (万元).
(万元).
(1)写出![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)当精加工蔬菜多少吨时,总利润最大,并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:4x-3y+6=0和直线l2:x=-![]() .若拋物线C:y2=2px(p>0)上的点到直线l1和直线l2的距离之和的最小值为2.
.若拋物线C:y2=2px(p>0)上的点到直线l1和直线l2的距离之和的最小值为2.
(1)求抛物线C的方程;
(2)若以拋物线上任意一点M为切点的直线l与直线l2交于点N,试问在x轴上是否存在定点Q,使Q点在以MN为直径的圆上,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市2011年至2017年新开楼盘的平均销售价格(单位:千元/平方米)的统计数据如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格 | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求![]() 关于x的线性回归方程;
关于x的线性回归方程;
(2)利用(1)中的回归方程,分析2011年至2017年该市新开楼盘平均销售价格的变化情况,并预测该市2019年新开楼盘的平均销售价格。
附:参考公式: 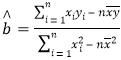 ,
,![]() ,其中
,其中![]() 为样本平均值。
为样本平均值。
参考数据:![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如下频率分布直方图(其中分组区间为![]() ,
,![]() ,…,
,…,![]() ).
).

(1)求成绩在![]() 的频率,并补全此频率分布直方图;
的频率,并补全此频率分布直方图;
(2)求这次考试平均分的估计值;
(3)若从成绩在![]() 和
和![]() 的学生中任选两人,求他们的成绩在同一分组区间的概率.
的学生中任选两人,求他们的成绩在同一分组区间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求k的值;
(2)设g(x)=log4![]() ,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)在如图所示给定的直角坐标系内画出f(x)的图象;
(2)写出f(x)的单调递增区间;
(3)由图象指出当x取什么值时f(x)有最值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com