7
分析:方程f
2(x)-f(x)=0可解出f(x)=0或f(x)=1,方程f
2(x)-f(x)=0的不相等的实根个数即两个函数f(x)=0或f(x)=1的所有不相等的根的个数的和,根据函数f(x)的形式,求方程的根的个数的问题可以转化为求两个函数y=0,y=1的图象与函数f(x)的图象的交点个数的问题.
解答:
解:方程f
2(x)-f(x)=0可解出f(x)=0或f(x)=1,
方程f
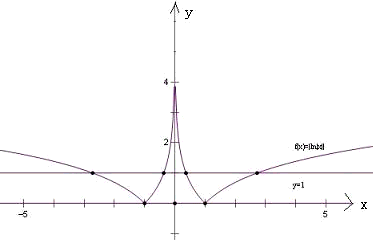
2(x)-f(x)=0的不相等的实根个数即两个函数f(x)=0或f(x)=1的所有不相等的根的个数的和,方程的根的个数与两个函数y=0,y=1的图象与函数
f(x)的图象的交点个数相同,
如图,由图象,y=1的图象与函数f(x)的图象的交点个数有四个,y=0的图象与函数f(x)的图象的交点个数有三个,
故方程f
2(x)-f(x)=0有七个解,
应选C.
点评:本题考点是分段函数,考查解分段函数类型的方程,求其根的个数,此类题常转化为求函数交点的个数,用图象法来求解.

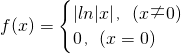 ,则方程f2(x)-f(x)=0不相等的实根的个数为________.
,则方程f2(x)-f(x)=0不相等的实根的个数为________. 解:方程f2(x)-f(x)=0可解出f(x)=0或f(x)=1,
解:方程f2(x)-f(x)=0可解出f(x)=0或f(x)=1,

 阅读快车系列答案
阅读快车系列答案