
在四棱锥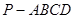 中,
中,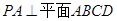 ,
,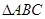 是正三角形,
是正三角形, 的交点
的交点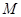 恰好是
恰好是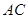 中点,又
中点,又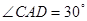 ,
,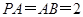 ,点
,点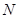 在线段
在线段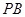 上,且
上,且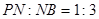 .
.

(1)求证: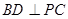 ;
;
(2)求证: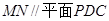 ;
;
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案科目:高中数学 来源:天利38套《2008全国各省市高考模拟试题汇编 精华大字版》、数学理 题型:013
在三棱锥P-ABC中,给出下列四个命题:
①若PA⊥BC,PB⊥AC,则PC⊥AB;
②若P到△ABC三边的距离相等,则P在底面上的射影O是△ABC的内心;
③若△ABC是正三角形,∠APB=∠BPC=∠CPA,则此三棱锥是正三棱锥;
④若三个侧面都是全等的等腰三角形,则此三棱锥是正三棱锥.
其中正确命题的个数是
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
①若PA⊥BC,PB⊥AC,则PC⊥AB;
②若P到△ABC三边的距离相等,则P在底面上的射影O是△ABC的内心;
③若△ABC是正三角形,∠APB=∠BPC=∠CPA,则此三棱锥是正三棱锥;
④若三个侧面都是全等的等腰三角形,则此三棱锥是正三棱锥.
其中正确命题的个数是 ( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2012-2013学年云南省昭通市毕业生复习统一检测文科数学试卷(解析版) 题型:解答题
如图,在正四棱锥 中,底面是边长为2的正方形,侧棱
中,底面是边长为2的正方形,侧棱 ,
, 为
为 的中点,
的中点, 是侧棱
是侧棱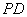 上的一动点。
上的一动点。

(1)证明: ;
;
(2)当直线 时,求三棱锥
时,求三棱锥 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:0116 期末题 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com