
| 1 |
| 3 |
|
| 1 |
| 2 |
| b |
| a |
| 3 |
| 2 |
| 2b |
| a |
| a-3b |
| a |
2
| ||
| |a| |
(
|
| 1 |
| 2 |
| b |
| a |
| 3 |
| 2 |
| 3, |
| 23 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 福建省第14届运动会在妈祖故里莆田举行,在开幕式表演“篮球操”的训练中我校A、B、C三个同学一组进行传球训练,每个同学传给另外两个中的某一个的可能性都相同
福建省第14届运动会在妈祖故里莆田举行,在开幕式表演“篮球操”的训练中我校A、B、C三个同学一组进行传球训练,每个同学传给另外两个中的某一个的可能性都相同查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
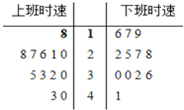 某市对上下班交通情况作抽样调查,作出上下班时间各抽取的12辆机动车行驶时速(单位:km/h)的茎叶图如图.则上、下班行驶时速的中位数分别为( )
某市对上下班交通情况作抽样调查,作出上下班时间各抽取的12辆机动车行驶时速(单位:km/h)的茎叶图如图.则上、下班行驶时速的中位数分别为( )| A、28与28.5 |
| B、29与28.5 |
| C、28与27.5 |
| D、29与27.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| x+1 |
| 4 |
| x-1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com