
若函数f(x)=a|2x-4|(a>0,a≠1)满足f(1)= ,则f(x)的单调递减区间是( )
,则f(x)的单调递减区间是( )
(A)(-∞,2] (B)[2,+∞)
(C)[-2,+∞) (D)(-∞,-2]
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(五)第二章第二节练习卷(解析版) 题型:解答题
已知f(x)= (x≠a).
(x≠a).
(1)若a=-2,试证f(x)在(-∞,-2)上单调递增.
(2)若a>0且f(x)在(1,+∞)上单调递减,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(三)第一章第三节练习卷(解析版) 题型:选择题
已知命题
p1:函数y=2x-2-x在R上为增函数,
p2:函数y=2x+2-x在R上为减函数,
则在命题q1:p1∨p2,q2:p1∧p2,q3:(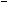 p1)∨p2和q4:p1∧(
p1)∨p2和q4:p1∧(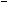 p2)中,真命题是( )
p2)中,真命题是( )
(A)q1,q3 (B)q2,q3 (C)q1,q4 (D)q2,q4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(七)第二章第四节练习卷(解析版) 题型:填空题
设定义在R上的函数f(x)同时满足以下条件:①f(x)+f(-x)=0;②f(x)=f(x+2);③当0≤x≤1时,f(x)=2x-1,则f( )+f(1)+f(
)+f(1)+f( )+f(2)+f(
)+f(2)+f( )
)
= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(七)第二章第四节练习卷(解析版) 题型:选择题
偶函数f (x)满足f(x-1)=f(x+1),且在x∈[0,1]时,f(x)=x,则关于x的方程f(x)=(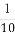 )x在x∈[0,4]上解的个数是( )
)x在x∈[0,4]上解的个数是( )
(A)1 (B)2 (C)3 (D)4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(一)第一章第一节练习卷(解析版) 题型:填空题
已知A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},B≠?,且B⊆A,则m的取值范围是___________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十四第七章第三节练习卷(解析版) 题型:选择题
如图,正三棱柱ABC-A1B1C1的各棱长(包括底面边长)都是2,E,F分别是AB,A1C1的中点,则EF与侧棱C1C所成的角的余弦值是( )
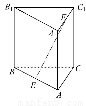
(A)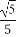 (B)
(B)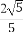 (C)
(C) (D)2
(D)2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十五第七章第四节练习卷(解析版) 题型:解答题
如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,点M在AD1上移动,点N在BD上移动,D1M=DN=a(0<a<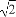 ),连接MN.
),连接MN.
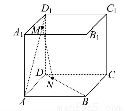
(1)证明对任意a∈(0,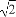 ),总有MN∥平面DCC1D1.
),总有MN∥平面DCC1D1.
(2)当a为何值时,MN的长最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com