练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知tan（π-x）=2，则sin2x+2sinxcosx=________．

    0
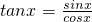
    分析：根据正切的诱导公式，得到tan（π-x）=-tanx=2，从而=-2，所以sinx=-2cosx，可得sinx+2cosx=0，最后代入sin2x+2sinxcosx即可．
    解答：∵tan（π-x）=-tanx=2
    ∴tanx=-2，
    又∵，
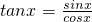
    ∴sinx=-2cosx，可得sinx+2cosx=0
    因此，sin2x+2sinxcosx=sinx（sinx+2cosx）=0
    故答案为：0
    点评：本题给出π-x的正切值，要我们求x的正弦平方与x的正弦、余弦积的二倍的和，着重考查了正切的诱导公式和同角三角函数的关系等知识点，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知tan（x-y）=2，tan(y+
    π
    5
    )    =3，则tan(x+
    π
    5
    )    =（　　）
    A、-2B、2C、-1D、1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知tan（π-x）=2，则sin2x+2sinxcosx=
    0
    0
    ．

    查看答案和解析>>

    科目：高中数学 来源：2010年高三数学高考预测系列试卷：选择题（解析版） 题型：选择题

    已知tan（x-y）=2，tan=3，则tan=（ ）
    A．-2
    B．2
    C．-1
    D．1

    查看答案和解析>>

    科目：高中数学 来源：0125 期末题 题型：解答题

    已知tan（x-）=（＜x＜），
    （1）求cosx的值；
    （2）求的值。

    查看答案和解析>>

    同步练习册答案