
 ,其中a≠0.
,其中a≠0.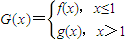 ,曲线y=G(x)上是否存在两点P、Q,使△OPQ(O为原点)是以O为直角顶点的直角三角形,且该三角形斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.
,曲线y=G(x)上是否存在两点P、Q,使△OPQ(O为原点)是以O为直角顶点的直角三角形,且该三角形斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.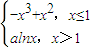 ,先假设曲线y=G(x)上存在满足题意的两点P、Q,易知P、Q两点在y轴两侧,由此可设P(t,G(t))(t>0)、Q(-t,t3+t2),由题意知∠POQ为直角,从而有
,先假设曲线y=G(x)上存在满足题意的两点P、Q,易知P、Q两点在y轴两侧,由此可设P(t,G(t))(t>0)、Q(-t,t3+t2),由题意知∠POQ为直角,从而有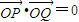 ,即-t2+G(t)(t3+t2)=0①.分(1)0<t≤1时,(2)t>1时两种情况进行讨论,此时可知G(t)表达式,(1)种情况易判断,(2)种情况分离出参数a后构造函数,转化为求函数值域可以解决;
,即-t2+G(t)(t3+t2)=0①.分(1)0<t≤1时,(2)t>1时两种情况进行讨论,此时可知G(t)表达式,(1)种情况易判断,(2)种情况分离出参数a后构造函数,转化为求函数值域可以解决; m+(4+m)=0,
m+(4+m)=0,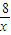 =
=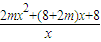 =
=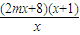 .
.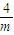 ,F′(x)<0,得x>-
,F′(x)<0,得x>-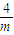 ,
,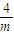 )上为增函数,在(
)上为增函数,在(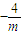 ,+∞)上为减函数,
,+∞)上为减函数,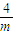 )上为增函数,在(
)上为增函数,在(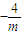 ,+∞)上为减函数.
,+∞)上为减函数.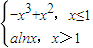 ,
,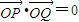 ,∴-t2+G(t)(t3+t2)=0①.
,∴-t2+G(t)(t3+t2)=0①.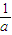 =(t+1)lnt,
=(t+1)lnt, +1,
+1, >0,∴a>0.
>0,∴a>0.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| π |
| 6 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省鄂州二中高三(上)10月段考数学试卷(解析版) 题型:解答题
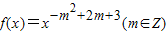 为偶函数,且在区间(0,+∞)上是单调增函数
为偶函数,且在区间(0,+∞)上是单调增函数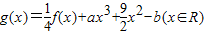 ,其中a,b∈R.若函数g(x)仅在x=0处有极值,求a的取值范围.
,其中a,b∈R.若函数g(x)仅在x=0处有极值,求a的取值范围.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
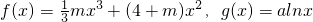 ,其中a≠0.
,其中a≠0.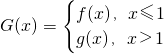 ,曲线y=G(x)上是否存在两点P、Q,使△OPQ(O为原点)是以O为直角顶点的直角三角形,且该三角形斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.
,曲线y=G(x)上是否存在两点P、Q,使△OPQ(O为原点)是以O为直角顶点的直角三角形,且该三角形斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:2013年山东省潍坊市高考数学一模试卷(理科)(解析版) 题型:解答题
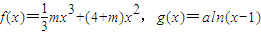 ,其中a≠0.
,其中a≠0.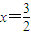 的对称点在y=f(x)的图象上,求m的值;
的对称点在y=f(x)的图象上,求m的值;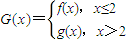 ,曲线y=G(x)上是否存在两点P、Q,使△OPQ(O为原点)是以O为直角顶点的直角三角形,且斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.
,曲线y=G(x)上是否存在两点P、Q,使△OPQ(O为原点)是以O为直角顶点的直角三角形,且斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com