Question

20．一架战斗机以1000$\sqrt{2}$千米/小时速度朝东偏北45°方向水平飞行，发现正东100千米外同高度有一架民航飞机正在以800千米/小时速度朝正北飞行，如双方都不改变速度与航向，两机最小距离在哪个区间内（单位：千米）（　　）

• A． （0，5）
• B． （5，10）
• C． （10，15）
• D． （15，20）

Answer 1

分析 建立如图所示的坐标系，t小时后，A（1000t，1000t），B（100，800t），求出|AB|，可得|AB|的最小值，即可得出结论．

解答 解：建立如图所示的坐标系，t小时后，A（1000t，1000t），B（100，800t），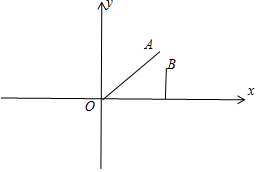
则|AB|=$\sqrt{（1000t-100）^{2}+40000{t}^{2}}$=$\sqrt{1040000{t}^{2}-200000t+10000}$，
t=$\frac{5}{52}$时，|AB|的最小值为$\sqrt{\frac{4×1040000×10000-20000{0}^{2}}{4×1040000}}$=$\frac{50\sqrt{26}}{13}$∈（15，20）．
故选D．

点评 本题考查坐标系的运用，考查距离公式，属于中档题．