
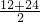 =18,
=18,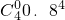 -
-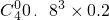 =
=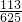 …(12分)
…(12分)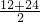 ,从而得出每支这种灯管的平均使用寿命;
,从而得出每支这种灯管的平均使用寿命;

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省佛山市高三教学质量检测(一)理科数学 题型:解答题
佛山某学校的场室统一使用“佛山照明”的一种灯管,已知这种灯管使用寿命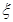 (单位:月)服从正态分布
(单位:月)服从正态分布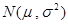 ,且使用寿命不少于
,且使用寿命不少于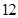 个月的概率为
个月的概率为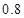 ,使用寿命不少于
,使用寿命不少于 个月的概率为
个月的概率为 .
.
(1)求这种灯管的平均使用寿命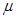 ;
;
(2)假设一间功能室一次性换上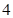 支这种新灯管,使用
支这种新灯管,使用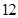 个月时进行一次检查,将已经损坏的灯管换下(中途不更换),求至少两支灯管需要更换的概率.
个月时进行一次检查,将已经损坏的灯管换下(中途不更换),求至少两支灯管需要更换的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
佛山某学校的场室统一使用“佛山照明”的一种灯管,已知这种灯管使用寿命![]() (单位:月)服从正态分布
(单位:月)服从正态分布![]() ,且使用寿命不少于
,且使用寿命不少于![]() 个月的概率为
个月的概率为![]() ,使用寿命不少于
,使用寿命不少于![]() 个月的概率为
个月的概率为![]() .
.
(1)求这种灯管的平均使用寿命![]() ;
;
(2)假设一间功能室一次性换上![]() 支这种新灯管,使用
支这种新灯管,使用![]() 个月时进行一次检查,将已经损坏的灯管换下(中途不更换),求至少两支灯管需要更换的概率.
个月时进行一次检查,将已经损坏的灯管换下(中途不更换),求至少两支灯管需要更换的概率.
查看答案和解析>>
科目:高中数学 来源:2012年广东省佛山市高考数学一模试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com