
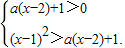 解集为非空集合,化简整理得
解集为非空集合,化简整理得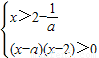 .接下来分三种情况加以讨论:①当1<a<2时,有
.接下来分三种情况加以讨论:①当1<a<2时,有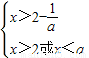 ,结合a>2-
,结合a>2-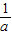 ,可得此时x的取值范围为(2-
,可得此时x的取值范围为(2-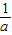 ,a)∪(2,+∞);②当a=2时,易得此时x的取值范围为(
,a)∪(2,+∞);②当a=2时,易得此时x的取值范围为( ,2)∪(2,+∞);③当a>2时,对照①的分析,可得此时x的取值范围为(2-
,2)∪(2,+∞);③当a>2时,对照①的分析,可得此时x的取值范围为(2-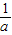 ,2)∪(a,+∞).
,2)∪(a,+∞).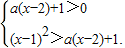 解集为非空集合,
解集为非空集合,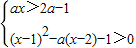 解集非空,结合已知条件a>1,解得
解集非空,结合已知条件a>1,解得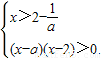 (4分)
(4分)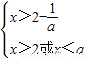 ,
,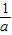 )=a+
)=a+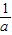 -2>0,即a>2-
-2>0,即a>2-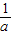 ,
,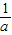 <x<a.
<x<a.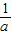 ,a)∪(2,+∞).(6分)
,a)∪(2,+∞).(6分) 且x≠2,此时x的取值范围为(
且x≠2,此时x的取值范围为( ,2)∪(2,+∞).(8分)
,2)∪(2,+∞).(8分)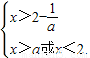 ⇒x>a或2-
⇒x>a或2-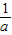 <x<2.(10分)
<x<2.(10分)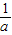 ,2)∪(a,+∞).(12分)
,2)∪(a,+∞).(12分)

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com