A
分析:因不等式x
2-(a+1)x+a<0的解集与a的取值有关,须对a进行分类讨论.由a≠1,则N为非空集合,N⊆M则说明N的元素是M的元素,由M={x|2x+1≥0}解出集合M后,易得到满足条件的实数a的范围即可.
解答:∵M={x|2x+1≥0}={x|x≥-

},
又∵不等式x
2-(a+1)x+a<0可化为(x-1)(x-a)<0,
①当a>1时,N={x|1<x<a}⊆M;
②当a=1时,N=∅⊆M;
③当a<1时,N={x|a<x<1},为了N⊆M;
∴a≥-

,
∴-

≤a<1.
综上所述,a≥-

故选A.
点评:本题考察的知识点是集合的包含关系判断及应用,集合N⊆M,说明N为空集或N的元素都为M的元素,本题中由a≠1,N≠∅,需要分类讨论,要分N=∅和N≠∅情况讨论.

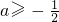
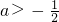
 },
}, ,
, ≤a<1.
≤a<1.

