
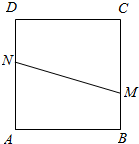
 ��ͼ���߳�Ϊ1������ABCD�У��ֱ��ڱ�BC��AD�ϸ�ȡһ��M��N�����������ģ��ķ�������|MN|��1.1�ĸ��ʣ����ü�����е����������������0��1֮������ʵ��x��y����BM=x��AN=y�����ȷ��M��N���λ�ã����������߶�MN�ij��ȣ���x��y������ԣ�x��y���������ģ�������20���������
��ͼ���߳�Ϊ1������ABCD�У��ֱ��ڱ�BC��AD�ϸ�ȡһ��M��N�����������ģ��ķ�������|MN|��1.1�ĸ��ʣ����ü�����е����������������0��1֮������ʵ��x��y����BM=x��AN=y�����ȷ��M��N���λ�ã����������߶�MN�ij��ȣ���x��y������ԣ�x��y���������ģ�������20���������| A�� | 0.3 | B�� | 0.35 | C�� | 0.65 | D�� | 0.7 |
���� �����⣬�����ģ�����������20����������������⣬����ͨ���оٵõ���7������������ݸ��ʹ�ʽ���õ������
��� �⣺�����⣬|MN|=$\sqrt{1+��y-x��^{2}}$��1.1���ࣨy-x��2��0.21��
20��������������������0.82��0.28������0.66��0.18������0.59��0.06������0.98��0.32������0.06��0.78������0.17��0.75������0.15��0.98������7����
�ࡰ|MN|��1.1���ĸ�����$\frac{7}{20}$=0.35��
��ѡ��B��
���� ���⿼��ģ�ⷽ�����Ƹ��ʣ���һ�������⣬��������Ŀ����Ҫ�����ǵȿ����¼��ĸ��ʣ�ע���оٷ��ڱ����Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -$\frac{1}{2}$ | C�� | -1��-$\frac{1}{2}$ | D�� | 1��-$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | A⊆B | B�� | A��B | C�� | A��B��ϵ | D�� | A?B |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
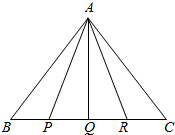 ��P��Q��R�DZ߳�Ϊ1������ABC��BC�ϵ��ĵȷֵ㣬��$\overrightarrow{AB}$•$\overrightarrow{AP}$+$\overrightarrow{AP}$•$\overrightarrow{AQ}$+$\overrightarrow{AQ}$•$\overrightarrow{AR}$+$\overrightarrow{AR}$•$\overrightarrow{AC}$=$\frac{13}{4}$��
��P��Q��R�DZ߳�Ϊ1������ABC��BC�ϵ��ĵȷֵ㣬��$\overrightarrow{AB}$•$\overrightarrow{AP}$+$\overrightarrow{AP}$•$\overrightarrow{AQ}$+$\overrightarrow{AQ}$•$\overrightarrow{AR}$+$\overrightarrow{AR}$•$\overrightarrow{AC}$=$\frac{13}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
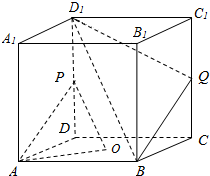 ��ͼ����������ABCD-A1B1C1D1�У�OΪ����ABCD�����ģ�P��Q�ֱ�����DD1��CC1���е㣮
��ͼ����������ABCD-A1B1C1D1�У�OΪ����ABCD�����ģ�P��Q�ֱ�����DD1��CC1���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �˶�Ա��� | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 |
| �÷� | 5 | 10 | 12 | 16 | 8 | 21 | 27 | 15 | 6 | 22 | 18 |
| �÷����� | Ƶ�� | Ƶ�� |
| [0��10�� | 3 | $\frac{1}{4}$ |
| [10��20�� | ||
| [20��30�� | ||
| �ϼ� | 12 | 1.00 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com