
设向量a=(cosα,sinα),b=(cosβ,sinβ),其中0<α<β<π,若|2a+b|=|a-2b|,则β-α=( )
A.![]() B.-
B.-![]()
C.![]() D.-
D.-![]()
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源:2004年高考教材全程总复习试卷·数学 题型:044
设向量a=(cos ,cos
,cos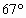 ),b=(cos
),b=(cos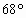 ,cos
,cos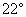 ),c=a+tb(t∈R)
),c=a+tb(t∈R)
(1)求a·b.
(2)求|c|的最小值.
查看答案和解析>>
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
设向量a=(cos![]() ,cos
,cos![]() ),b=(cos
),b=(cos![]() ,cos
,cos![]() ),u=a+tb(t∈R).
),u=a+tb(t∈R).
(1)求a·b;
(2)求u的模的最小值.
查看答案和解析>>
科目:高中数学 来源:江苏省启东中学2009届高三数学高考模拟试卷(五) 题型:044
设向量a=(cosα,sinα),![]() ,c=a+tb(t∈R),其中α为锐角.
,c=a+tb(t∈R),其中α为锐角.
(1)求a·b;
(2)当t为何值时,c的模最小?最小值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
设向量a=(cos 55°,sin 55°),b=![]() (cos 25°,sin 25°),若t是实数,则|a-tb|的最小值为( )
(cos 25°,sin 25°),若t是实数,则|a-tb|的最小值为( )
A.![]() B.
B.![]()
C.1 D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com