
���� ��I������б��Ϊ$\frac{��}{3}$���Ҿ�������P��0��1����ֱ��l�IJ�������Ϊ��$\left\{\begin{array}{l}{x=tcos\frac{��}{3}}\\{y=1+tsin\frac{��}{3}}\end{array}\right.$������C�ļ����귽�̦�=2$\sqrt{2}$sin����+$\frac{��}{4}$����չ������2=2$\sqrt{2}��$��$\frac{\sqrt{2}}{2}$��sin��+cos�ȣ������û�����ʽ�ɵ�ֱ�����귽�̣�
��II����ֱ��l�IJ�������$\left\{\begin{array}{l}{x=\frac{1}{2}t}\\{y=1+\frac{\sqrt{3}}{2}t}\end{array}\right.$����ԲC�ķ���Ϊ��t2-t-1=0���ɵ�$\frac{1}{|PM|}$+$\frac{1}{|PN|}$=$\frac{1}{|{t}_{1}|}$+$\frac{1}{|{t}_{2}|}$=$\frac{|{t}_{1}-{t}_{2}|}{|{t}_{1}{t}_{2}|}$=$\frac{\sqrt{��{t}_{1}+{t}_{2}��^{2}-4{t}_{1}{t}_{2}}}{|{t}_{1}{t}_{2}|}$���ɵó���
��� �⣺��I������б��Ϊ$\frac{��}{3}$���Ҿ�������P��0��1����ֱ��l�IJ�������Ϊ��$\left\{\begin{array}{l}{x=tcos\frac{��}{3}}\\{y=1+tsin\frac{��}{3}}\end{array}\right.$����Ϊ��$\left\{\begin{array}{l}{x=\frac{1}{2}t}\\{y=1+\frac{\sqrt{3}}{2}t}\end{array}\right.$��
����C�ļ����귽�̦�=2$\sqrt{2}$sin����+$\frac{��}{4}$����չ������2=2$\sqrt{2}��$��$\frac{\sqrt{2}}{2}$��sin��+cos�ȣ����ɵ�ֱ�����귽�̣�x2+y2=2x+2y��
��II����ֱ��l�IJ�������$\left\{\begin{array}{l}{x=\frac{1}{2}t}\\{y=1+\frac{\sqrt{3}}{2}t}\end{array}\right.$����ԲC�ķ���Ϊ��t2-t-1=0��
t1+t2=1��t1t2=-1��
��$\frac{1}{|PM|}$+$\frac{1}{|PN|}$=$\frac{1}{|{t}_{1}|}$+$\frac{1}{|{t}_{2}|}$=$\frac{|{t}_{1}-{t}_{2}|}{|{t}_{1}{t}_{2}|}$=$\frac{\sqrt{��{t}_{1}+{t}_{2}��^{2}-4{t}_{1}{t}_{2}}}{|{t}_{1}{t}_{2}|}$=$\frac{\sqrt{1+4}}{1}$=$\sqrt{5}$��
���� ���⿼���˼����귽�̻�Ϊֱ�����귽�̡��������̻�Ϊ��ͨ���̡�ֱ����Բ�ཻ�ҳ����⣬������������������������������е��⣮


 �߽�������ϵ�д�
�߽�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ����������֢ | ����������֢ | �ϼ� | |
| �� | 35 | 25 | 60 |
| Ů | 30 | 10 | 40 |
| �ܼ� | 65 | 35 | 100 |
| P��K2��k0�� | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
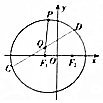 һ�Ű뾶Ϊ4��Բ��ֽƬ��Բ��ΪF1��F2��Բ��һ�����㣬��F1F2=2��P��Բ��һ�����㣬��ֽƬ�۵�ʹ��F2��P�غϣ�Ȼ��ĨƽֽƬ���ۺ�ΪCD����CD��뾶PF1�Ľ���ΪQ����P��Բ���˶�ʱ����Q��Ĺ켣Ϊ����E����F1F2����ֱ��xΪ�ᣬF1F2���д���Ϊy�Ὠ��ƽ��ֱ������ϵ����ͼ��
һ�Ű뾶Ϊ4��Բ��ֽƬ��Բ��ΪF1��F2��Բ��һ�����㣬��F1F2=2��P��Բ��һ�����㣬��ֽƬ�۵�ʹ��F2��P�غϣ�Ȼ��ĨƽֽƬ���ۺ�ΪCD����CD��뾶PF1�Ľ���ΪQ����P��Բ���˶�ʱ����Q��Ĺ켣Ϊ����E����F1F2����ֱ��xΪ�ᣬF1F2���д���Ϊy�Ὠ��ƽ��ֱ������ϵ����ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com