
【题目】已知函数f(x)=eax﹣x﹣1,其中a≠0.若对一切x∈R,f(x)≥0恒成立,则a的取值集合 .
【答案】{1}
【解析】解:若a<0,则对一切x>0,∵eax<1,∴f(x)=eax﹣x﹣1<0,这与题设矛盾.又a≠0,故a>0.
而f′(x)=aeax﹣1,令f′(x)=0得x= ![]() ln
ln ![]() ,
,
当x< ![]() ln
ln ![]() 时,f′(x)<0,f(x)单调递减;
时,f′(x)<0,f(x)单调递减;
当x> ![]() ln
ln ![]() 时,f′(x)>0,f(x)单调递增.
时,f′(x)>0,f(x)单调递增.
∴当x= ![]() ln
ln ![]() ,f(x)取最小值f(
,f(x)取最小值f( ![]() ln
ln ![]() )=
)= ![]() ﹣
﹣ ![]() ln
ln ![]() ﹣1.
﹣1.
于是对一切x∈R,f(x)≥0恒成立,当且仅当 ![]() ﹣
﹣ ![]() ln
ln ![]() ﹣1≥0.①
﹣1≥0.①
令g(t)=t﹣tlnt﹣1,(t= ![]() )则g′(t)=﹣lnt,
)则g′(t)=﹣lnt,
当0<t<1时,g′(t)>0,g(t)单调递增;
当t>1时,g′(t)<0,g(t)单调递减,
∴当t=1时,g(t)取最大值g(1)=1﹣1=0.
∴当且仅当 ![]() =1,即a=1时,①式等号成立.
=1,即a=1时,①式等号成立.
综上所述,a的取值集合为{1}.
所以答案是:{1}.
【考点精析】解答此题的关键在于理解函数的最大(小)值与导数的相关知识,掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是( ) 
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() ]
]
C.( ![]() ,
, ![]() ]
]
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在区间(﹣1,1)上的增函数f(x)= ![]() 为奇函数,且f(
为奇函数,且f( ![]() )=
)= ![]()
(1)求函数f(x)的解析式;
(2)解关于t的不等式f(t﹣1)+f(t)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosωx﹣sinωx,sinωx),
=(cosωx﹣sinωx,sinωx), ![]() =(﹣cosωx﹣sinωx,2
=(﹣cosωx﹣sinωx,2 ![]() cosωx),设函数f(x)=
cosωx),设函数f(x)= ![]() +λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(
+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈( ![]() ,1)
,1)
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点( ![]() ,0)求函数f(x)在区间[0,
,0)求函数f(x)在区间[0, ![]() ]上的取值范围.
]上的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程  (t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为:ρ=4cosθ.
(t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为:ρ=4cosθ.
(1)把直线l的参数方程化为极坐标方程,把曲线C的极坐标方程化为普通方程;
(2)求直线l与曲线C交点的极坐标(ρ≥0,0≤θ<2π).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是( ) 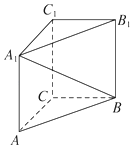
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点A,B是单位圆O上的两点,A,B点分别在第一,而象限,点C是圆O与x轴正半轴的交点,若∠COA=60°,∠AOB=α,点B的坐标为(﹣ ![]() ,
, ![]() ).
). 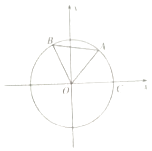
(1)求sinα的值;
(2)已知动点P沿圆弧从C点到A点匀速运动需要2秒钟,求动点P从A点开始逆时针方向作圆周运动时,点P的纵坐标y关于时间t(秒)的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com