
【题目】若x>0,则函数 ![]() 与y2=logax(a>0,且a≠1)在同一坐标系上的部分图象只可能是( )
与y2=logax(a>0,且a≠1)在同一坐标系上的部分图象只可能是( )
A.
B.
C.
D.
【答案】B
【解析】解:当a>1时,
函数 ![]() 为增函数,且图象过(0,﹣1)点,向右和x轴无限接近,
为增函数,且图象过(0,﹣1)点,向右和x轴无限接近,
函数y2=logax(a>0,且a≠1)为增函数,且图象过(1,0)点,向左和y轴无限接近,
此时答案B符合要求,
当0<a<1时,
函数 ![]() 为减函数,且图象过(0,﹣1)点,
为减函数,且图象过(0,﹣1)点,
函数y2=logax(a>0,且a≠1)为减函数,且图象过(1,0)点,向左和y轴无限接近,
此时无满足条件的图象.
故选:B
【考点精析】根据题目的已知条件,利用函数的图象的相关知识可以得到问题的答案,需要掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点.
(Ⅰ)求证:平面EAC⊥平面PBC;
(Ⅱ)若二面角P﹣AC﹣E的余弦值为 ![]() ,求直线PA与平面EAC所成角的正弦值.
,求直线PA与平面EAC所成角的正弦值.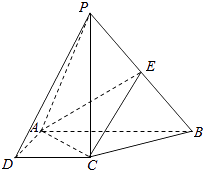
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某营养师要求为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营状中至少含64个单位的碳水化合物和42个单位的蛋白质和54个单位的维生素C.如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]. 
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如表所示,求数学成绩在[50,90)之外的人数.
分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
x:y | 1:1 | 2:1 | 3:4 | 4:5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应边分别是a,b,c,c=2,sin2A+sin2B﹣sin2C=sinAsinB.
(1)若sinC+sin(B﹣A)=2sin2A,求△ABC面积;
(2)求AB边上的中线长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+(y﹣1)2=9,直线l:x﹣my+m﹣2=0,且直线l与圆C相交于A、B两点. (Ⅰ)若|AB|=4 ![]() ,求直线l的倾斜角;
,求直线l的倾斜角;
(Ⅱ)若点P(2,1)满足 ![]() =
= ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|2a﹣x|+2x,a∈R.
(1)若a=0,判断函数y=f(x)的奇偶性,并加以证明;
(2)若函数f(x)在R上是增函数,求实数a的取值范围;
(3)若存在实数a∈[﹣2,2],使得关于x的方程f(x)﹣tf(2a)=0有三个不相等的实数根,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com