
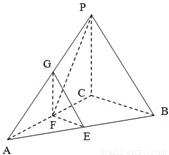
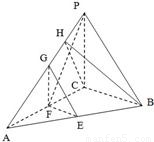
 (Ⅱ)解:过点C在平面PAC内作CH⊥PA,垂足为H.
(Ⅱ)解:过点C在平面PAC内作CH⊥PA,垂足为H.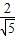 .
.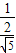 =
=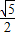 .
.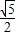 .
.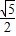 .(8分)
.(8分)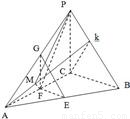 (Ⅲ)解法1:如图,设PB的中点为K,
(Ⅲ)解法1:如图,设PB的中点为K,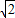 ,FM=
,FM= .
.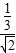 =
=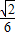 .
.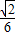 .
.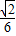 .(13分)
.(13分)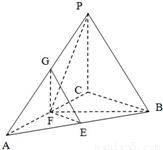 (Ⅲ)解法2:连接FB,
(Ⅲ)解法2:连接FB, ×PC×(
×PC×( ×AF×BC)
×AF×BC) ×1×(
×1×( ×1×1)=
×1×1)= .
. ×h×S△PAB(其中h是点F到平面PAB的距离)
×h×S△PAB(其中h是点F到平面PAB的距离) ×h×(
×h×( ×
×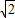 ×
×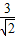 )=
)= ×h×
×h× =
= h,
h, =
= h解得h=
h解得h= .(11分)
.(11分)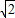 ,
,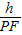 =
=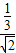 =
=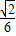 .
.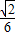 .
.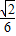 .(13分)
.(13分)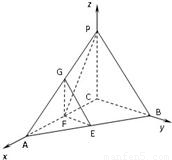 方法2:依条件建立如图所示空间直角坐标系C-xyz.
方法2:依条件建立如图所示空间直角坐标系C-xyz.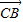 =(0,1,0)是平面PAC的一
=(0,1,0)是平面PAC的一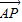 =(-2,0,1),
=(-2,0,1),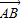 =(-2,1,0),
=(-2,1,0),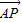 =0,n•
=0,n•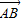 =0解得n=(1,2,2).(6分)
=0解得n=(1,2,2).(6分)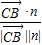 =
= .
. .(arccos
.(arccos =arctan
=arctan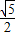 )(8分)
)(8分)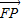 =(-1,0,1),
=(-1,0,1),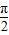 -α)=
-α)=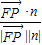 =
=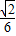 .(11分)
.(11分)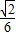 .
.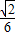 .
.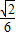 .(13分)
.(13分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
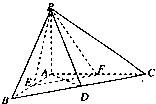
 如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.
如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=
如图,在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
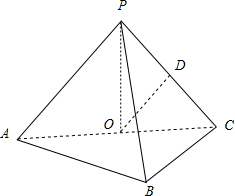 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
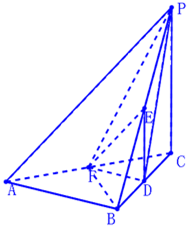 如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.
如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com