
分析 (Ⅰ)由三角函数公式化简可得f(x)=$sin(2x+\frac{π}{6})+\frac{1}{2}+a$,由周期公式可得周期,由图象过点$(\frac{π}{6},1)$可得a值;
(Ⅱ)由$0≤x≤\frac{π}{2}$和解析式结合三角函数的最值可得.
解答 解:(Ⅰ)由三角函数公式化简可得$f(x)={cos^2}x+\sqrt{3}sinxcosx+a$
=$\frac{1+cos2x}{2}+\frac{{\sqrt{3}sin2x}}{2}+a$=$sin(2x+\frac{π}{6})+\frac{1}{2}+a$.
∵函数f(x)的图象过点$(\frac{π}{6},1)$,
∴$f(\frac{π}{6})=sin(2×\frac{π}{6}+\frac{π}{6})+\frac{1}{2}+a=1$.解得$a=-\frac{1}{2}$.
∴函数f(x)的最小正周期为π;
(Ⅱ)∵$0≤x≤\frac{π}{2}$,∴$\frac{π}{6}≤2x+\frac{π}{6}≤\frac{7π}{6}$.
∴$-\frac{1}{2}≤sin(2x+\frac{π}{6})≤1$.
∴当$2x+\frac{π}{6}=\frac{7π}{6}$即$x=\frac{π}{2}$时,函数f(x)取最小值$-\frac{1}{2}$
点评 本题考查三角函数恒等变换,涉及三角函数的周期性和最值,属基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{34}{103}$ | B. | 100 | C. | $\frac{1}{100}$ | D. | $\frac{1}{104}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
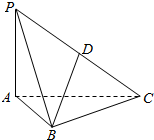 如图,PA⊥平面ABC,PA=$\sqrt{2}$,AB=1,BC=$\sqrt{3}$,AC=2,D是PC的中点.
如图,PA⊥平面ABC,PA=$\sqrt{2}$,AB=1,BC=$\sqrt{3}$,AC=2,D是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 《九章算术》中将底面的长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为蟞臑.在如图所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD=BC,则当点E在下列四个位置:PA中点、PB中点、PC中点、PD中点时分别形成的四面体E-BCD中,蟞臑有( )
《九章算术》中将底面的长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为蟞臑.在如图所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD=BC,则当点E在下列四个位置:PA中点、PB中点、PC中点、PD中点时分别形成的四面体E-BCD中,蟞臑有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p是特称命题,¬p:存在一条抛物线的离心率不为1 | |
| B. | p是特称命题,¬p:存在一条抛物线的离心率为1 | |
| C. | p是全称命题,¬p:存在一条抛物线的离心率不为1 | |
| D. | p是全称命题,¬p:存在一条抛物线的离心率为1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com