
为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)= 若不建隔热层(即x=0时),每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
若不建隔热层(即x=0时),每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值;
(2)求f(x)的表达式;
(3)利用“函数 (其中
(其中 为大于0的常数),在
为大于0的常数),在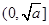 上是减函数,在
上是减函数,在 上是增函数”这一性质,求隔热层修建多厚时,总费用f(x)达到最小,并求出这个最小值.
上是增函数”这一性质,求隔热层修建多厚时,总费用f(x)达到最小,并求出这个最小值.
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:解答题
某企业在第1年初购买一台价值为120万元的设备M,M的价值在使用过程中逐年减少.从第2年到第6年,每年初M的价值比上年初减少10万元;从第7年开始,每年初M的价值为上年初的75%.
(1)求第n年初M的价值an的表达式;
(2)求数列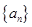 的前n项和
的前n项和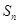
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
建造一断面为等腰梯形的防洪堤(如图),梯形的腰与底边所角为60°,考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为 m2,为了使堤的上面与两侧面的水泥用料最省,要求断面的外周长(梯形的上底BC与两腰长的和)最小.如何设计防洪堤,才能使水泥用料最省.
m2,为了使堤的上面与两侧面的水泥用料最省,要求断面的外周长(梯形的上底BC与两腰长的和)最小.如何设计防洪堤,才能使水泥用料最省.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
国家助学贷款是由财政贴息的信用贷款,旨在帮助高校家庭经济困难学生支付在校期间所需的学费、住宿费及生活费。每一年度申请总额不超过6000元。某大学2012届毕业生凌霄在本科期间共申请了24000元助学贷款,并承诺毕业后3年(按36个月计)内还清。签约单位提供的工资标准为第一年内每月1500元,第13个月开始每月工资比前一个月增加5%直到4000元。凌霄同学计划前12个月每月还款500元,第13个月开始每月还款比前一个月多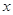 元.
元.
(1)若凌霄同学恰好在第36个月(即毕业后3年)还清贷款,求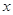 值;(6分)
值;(6分)
(2)当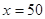 时,凌霄同学将在毕业后第几个月还清最后一笔贷款?他当月工资余额能否满足当月3000元的基本生活费?(6分)
时,凌霄同学将在毕业后第几个月还清最后一笔贷款?他当月工资余额能否满足当月3000元的基本生活费?(6分)
(参考数据: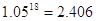 ,
,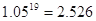 ,
,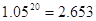 ,
, 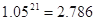 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,在
,在 时取得极值.
时取得极值.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若 时,
时, 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(Ⅲ)若 ,是否存在实数b,使得方程
,是否存在实数b,使得方程 在区间
在区间 上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知A、B两地的路程为240千米.某经销商每天都要用汽车或火车将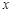 吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.
吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.
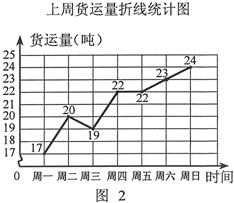
现有货运收费项目及收费标准表、行驶路程s(千米)与行驶时间t(时)的函数图象(如图1)、上周货运量折线统计图(如图2)等信息如下:
货运收费项目及收费标准表
| 运输工具 | 运输费单价:元/(吨•千米) | 冷藏费单价:元/(吨•时) | 固定费用:元/次 |
| 汽车 | 2 | 5 | 200 |
| 火车 | 1.6 | 5 | 2280 |
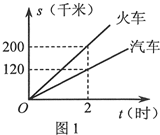
 汽(元)和
汽(元)和 火(元),分别求
火(元),分别求 汽、
汽、 火与
火与 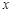 的函数关系式(不必写出
的函数关系式(不必写出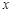 的取值范围),及
的取值范围),及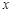 为何值时
为何值时 汽>
汽> 火(总费用=运输费+冷藏费+固定费用)
火(总费用=运输费+冷藏费+固定费用)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商店经销一种奥运会纪念品,每件产品的成本为30元,并且每卖出一件产品需向税务部门上交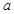 元(
元(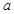 为常数,2≤a≤5 )的税收。设每件产品的售价为x元(35≤x≤41),根据市场调查,日销售量与
为常数,2≤a≤5 )的税收。设每件产品的售价为x元(35≤x≤41),根据市场调查,日销售量与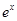 (e为自然对数的底数)成反比例。已知每件产品的日售价为40元时,日销售量为10件。
(e为自然对数的底数)成反比例。已知每件产品的日售价为40元时,日销售量为10件。
(1)求该商店的日利润L(x)元与每件产品的日售价x元的函数关系式;
(2)当每件产品的日售价为多少元时,该商品的日利润L(x)最大,并求出L(x)的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
列车提速可以提高铁路运输量.列车运行时,前后两车必须要保持一个“安全间隔距离d(千米)”,“安全间隔距离d(千米)”与列车的速度v(千米/小时)的平方成正比(比例系数k=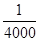 ).假设所有的列车长度l均为0.4千米,最大速度均为v0(千米/小时).问:列车车速多大时,单位时间流量Q=
).假设所有的列车长度l均为0.4千米,最大速度均为v0(千米/小时).问:列车车速多大时,单位时间流量Q=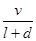 最大?
最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com