
【题目】如图所示,正方形![]() 与直角梯形
与直角梯形![]() 所在平面互相垂直,
所在平面互相垂直, ![]() ,
, ![]() ,
, ![]() .
.
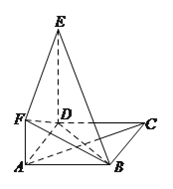
(I)求证: ![]() 平面
平面![]() .
.
(II)求证: ![]() 平面
平面![]() .
.
(III)求四面体![]() 的体积.
的体积.
【答案】(1)见解析(2)见解析(3)![]()
【解析】试题分析:(1)欲证AC⊥平面BDE,只需证明AC垂直平面BDE中的两条相交直线即可,因为AC与BD是正方形ABCD的对角线,所以AC⊥BD,再正DE垂直AC所在的平面,得到AC垂直DE,而BD,DE是平面BDE中的两条相交直线,问题得证.
(2)欲证AC∥平面BEF,只需证明AC平行平面BEF中的一条直线即可,利用中位线的性质证明OG平行DE且等于DE的一半,根据已知AF平行DE且等于DE的一半,所以OG与AF平行且相等,就可得到AC平行FG,而FG为平面BEF中的一条直线,问题得证.
(3)四面体BDEF可以看做以△DEF为底面,以点B为顶点的三棱锥,底面三角形DEF的底边DE=2,高DA=2,三棱锥的高为AB,长度等于2,再代入三棱锥的体积公式即可.
(![]() )因为平面
)因为平面![]() 平面
平面![]() ,
, ![]() ,
,
即![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() 是正方形,所以
是正方形,所以![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() .
.
(![]() )设
)设![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() ,如下图:
,如下图:
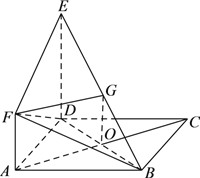
所以![]() 平行且等于
平行且等于![]() ,
,
因为![]() ,
, ![]() ,
,
所以![]() 平行且等于
平行且等于![]() ,从而四边形
,从而四边形![]() 是平行四边形,
是平行四边形,
![]() ,因为
,因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
即![]() 平面
平面![]() .
.
(![]() )
)![]() ,
, ![]() ,
,
因此四面体![]() 的体积
的体积![]() .
.


科目:高中数学 来源: 题型:
【题目】已知集合A={x|﹣2≤x<5},B={x|3x﹣5≥x﹣1}.
(1)求A∩B;
(2)若集合C={x|﹣x+m>0},且A∪C=C,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆的短轴端点与双曲线
,椭圆的短轴端点与双曲线![]() 的焦点重合,过点
的焦点重合,过点![]() 且不垂直于
且不垂直于![]() 轴的直线
轴的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
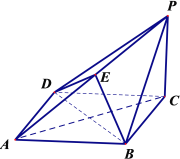
【题目】如图,在四棱锥![]() 中, 底面
中, 底面![]() 为菱形,
为菱形,![]() 平面
平面![]() ,点
,点![]() 在棱
在棱![]() 上.
上.
(Ⅰ)求证:直线![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 平面
平面![]() ,求证:
,求证:![]() ;
;
(Ⅲ)是否存在点![]() ,使得四面体
,使得四面体![]() 的体积等于四面体
的体积等于四面体![]() 的体积的
的体积的![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
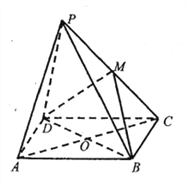
【题目】如图,点![]() 是菱形
是菱形![]() 所在平面外一点,
所在平面外一点, ![]() ,
, ![]() 是等边三角形,
是等边三角形, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 的所成角的大小.
的所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据如图给出的2004年至2013年我国二氧化硫年排放量(单位:万吨)柱形图,以下结论中不正确的是( ) 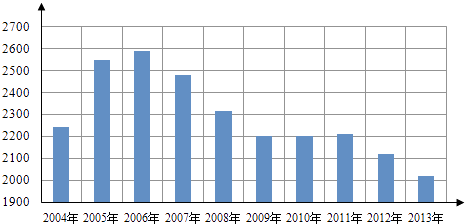
A.逐年比较,2008年减少二氧化硫排放量的效果最显著
B.2007年我国治理二氧化硫排放显现成效
C.2006年以来我国二氧化硫年排放量呈减少趋势
D.2006年以来我国二氧化硫年排放量与年份正相关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,
中, ![]() 为棱
为棱![]() 上一动点,
上一动点, ![]() 为底面
为底面![]() 上一动点,
上一动点, ![]() 是
是![]() 的中点,若点
的中点,若点![]() 都运动时,点
都运动时,点![]() 构成的点集是一个空间几何体,则这个几何体是
构成的点集是一个空间几何体,则这个几何体是
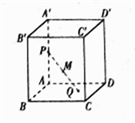
A. 棱柱 B. 棱台 C. 棱锥 D. 球的一部分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率为40%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器算出0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示没有命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了20组随机数:
907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A. 0.35 B. 0.25
C. 0,20 D. 0.15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com