
【题目】在正方体![]() 中,
中, ![]() 为棱
为棱![]() 上一动点,
上一动点, ![]() 为底面
为底面![]() 上一动点,
上一动点, ![]() 是
是![]() 的中点,若点
的中点,若点![]() 都运动时,点
都运动时,点![]() 构成的点集是一个空间几何体,则这个几何体是
构成的点集是一个空间几何体,则这个几何体是
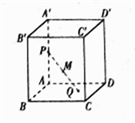
A. 棱柱 B. 棱台 C. 棱锥 D. 球的一部分
【答案】A
【解析】由题意知,当P在A′处,Q在AB上运动时,M的轨迹为过AA′的中点,在平面AA′B′B内平行于AB的线段(靠近AA′),当P在A′处,Q在AD上运动时,M的轨迹为过AA′的中点,在平面AA′D′D内平行于AD的线段(靠近AA′),
当Q在B处,P在AA′上运动时,M的轨迹为过AB的中点,在平面AA′B′B内平行于AA′的线段(靠近AB),
当Q在D处,P在AA′上运动时,M的轨迹为过AD的中点,在平面AA′B′B内平行于AA′的线段(靠近AD),
当P在A处,Q在BC上运动时,M的轨迹为过AB的中点,在平面ABCD内平行于AD的线段(靠近AB),
当P在A处,Q在CD上运动时,M的轨迹为过AD的中点,在平面ABCD内平行于AB的线段(靠近AB),
同理得到:P在A′处,Q在BC上运动;P在A′处,Q在CD上运动;P在A′处,Q在C处,P在AA′上运动;
P、Q都在AB,AD,AA′上运动的轨迹.进一步分析其它情形即可得到M的轨迹为棱柱体.
故选:A.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】【2015高考湖北(理)20】某厂用鲜牛奶在某台设备上生产![]() 两种奶制品.生产1吨
两种奶制品.生产1吨![]() 产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨
产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨![]() 产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天
产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天![]() 产品的产量不超过
产品的产量不超过![]() 产品产量的2倍,设备每天生产
产品产量的2倍,设备每天生产![]() 两种产品时间之和不超过12小时. 假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为
两种产品时间之和不超过12小时. 假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为
W | 12 | 15 | 18 |
P | 0.3 | 0.5 | 0.2 |
该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利![]() (单位:元)是一个随机变量.
(单位:元)是一个随机变量.
(Ⅰ)求![]() 的分布列和均值;
的分布列和均值;
(Ⅱ) 若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等腰直角三角形ABC的直角顶点A在x轴的正半轴上,B在y轴的正半轴上,C在第一象限,设∠BAO=θ(O为坐标原点),AB=AC=2,当OC的长取得最大值时,tanθ的值为( )
A.![]()
B.﹣1+ ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国Ⅳ标准规定:轻型汽车的屡氧化物排放量不得超过80mg/km.根据这个标准,检测单位从某出租车公司运营的A、B两种型号的出租车中分别抽取5辆,对其氮氧化物的排放量进行检测,检测结果记录如表(单位:mg/km)
A | 85 | 80 | 85 | 60 | 90 |
B | 70 | x | 95 | y | 75 |
由于表格被污损,数据x,y看不清,统计员只记得A、B两种出租车的氮氧化物排放量的平均值相等,方差也相等.
(1)求表格中x与y的值;
(2)从被检测的5辆B种型号的出租车中任取2辆,记“氮氧化物排放量超过80mg/km”的车辆数为X,求X=1时的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sin2x+2cos2x+m(0≤x≤
sin2x+2cos2x+m(0≤x≤ ![]() ).
).
(1)若函数f(x)的最大值为6,求常数m的值;
(2)若函数f(x)有两个零点x1和x2 , 求m的取值范围,并求x1和x2的值;
(3)在(1)的条件下,若g(x)=(t﹣1)f(x)﹣ ![]() (t≥2),讨论函数g(x)的零点个数.
(t≥2),讨论函数g(x)的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( ) 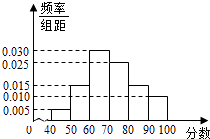
A.588
B.480
C.450
D.120
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() ,左焦点是
,左焦点是![]() .
.
(1)若左焦点![]() 与椭圆
与椭圆![]() 的短轴的两个端点是正三角形的三个顶点,点
的短轴的两个端点是正三角形的三个顶点,点![]() 在椭圆
在椭圆![]() 上.求椭圆
上.求椭圆![]() 的方程;
的方程;
(2)过原点且斜率为![]() 的直线
的直线![]() 与(1)中的椭圆
与(1)中的椭圆![]() 交于不同的两点
交于不同的两点![]() ,设
,设![]() ,求四边形
,求四边形![]() 的面积取得最大值时直线
的面积取得最大值时直线![]() 的方程;
的方程;
(3)过左焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,直线
两点,直线![]() 交直线
交直线![]() 于点
于点![]() ,其中
,其中![]() 是常数,设
是常数,设![]() ,
, ![]() ,计算
,计算![]() 的值(用
的值(用![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com