练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    甲、乙二人参加知识竞答，共有10个不同的题目，其中选择题6个，判断题4个，甲、乙二人依次各抽一题,那么
    (1)甲抽到选择题，乙抽到判断题的概率是多少?
    (2)甲、乙二人中至少有一个抽到选择题的概率是多少?

    解析试题分析：由题意知本题可以看做等可能事件的概率，试验发生包含的事件数10×9，（1）满足条件的事件是甲抽到选择题，乙抽到判断题，共有24种结果，即可求出概率；（2）满足条件的事件是甲、乙二人中至少有一人抽到选择题，的对立事件为甲、乙二人依次都抽到判断题，此概率为，根据对立事件的概率公式即可得到甲、乙二人中至少有一人抽到选择题的概率为1-，即可求出结果．
    解：(1)甲从选择题中抽到一题的可能结果有6个，乙从判断题中抽到一题的可能结果有4个，又甲、乙依次抽一题的结果共有10×9个，所以甲抽到选择题，乙抽到判断题的概率是：＝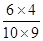
    (2)甲、乙二人依次都抽到判断题的概率为，故甲、乙二人中至少有一人抽到选择题的概率为1-＝．                          5′
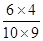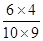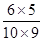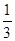    或： ++＝++＝，所求概率为．
    考点：古典概型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中，随机抽取了100名电视观众，相关的数据如下表所示：

     
    		文艺节目
    		新闻节目
    		总计
    20至40岁
    		40
    		18
    		58
    大于40岁
    		15
    		27
    		42
    总计
    		55
    		45
    		100
     
    (1)由表中数据直观分析，收看新闻节目的观众是否与年龄有关？
    (2)用分层抽样方法在收看新闻节目的观众中随机抽取5名，大于40岁的观众应该抽取几名？
    (3)在上述抽取的5名观众中任取2名，求恰有1名观众的年龄为20至40岁的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    (本小题满分9分)一个袋子中有3个红球和2个黄球，5个球除颜色外完全相同，甲、乙两人先后不放回地从中各取1个球.规定：若两人取得的球的颜色相同则甲获胜，否则乙获胜.
    (1) 求两个人都取到黄球的概率；
    (2) 计算甲获胜的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    甲、乙两个篮球运动员互不影响地在同一位置投球，命中率分别为与，且乙投球次均未命中的概率为．
    （1）求乙投球的命中率；
    （2）若甲投球次，乙投球次，两人共命中的次数记为，求的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    近年空气质量逐步恶化，雾霾天气现象出现增多，大气污染危害加重，大气污染可引起心悸、呼吸困难等心肺疾病．为了解某市心肺疾病是否与性别有关，在某医院随机对入院的50人进行了问卷调查得到了如下的列联表：

     
    		患心肺疾病
    		不患心肺疾病
    		合计
    男
    		 
    		5
    		 
    女
    		10
    		 
    		 
    合计
    		 
    		 
    		50
     
    已知在全部50人中随机抽取1人，抽到患心肺疾病的人的概率为．
    (1)请将上面的列联表补充完整；
    (2)是否有99．5%的把握认为患心肺疾病与性别有关？说明你的理由；
    临界值表供参考：
    P(K2≥k)
    		0．15
    		0．10
    		0．05
    		0．025
    		0．010
    		0．005
    		0．001
    k
    		2．072
    		2．706
    		3．841
    		5．024
    		6．635
    		7．879
    		10．828
     
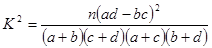    参考公式：其中

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    受轿车在保修期内维修费等因素的影响，企业生产每辆轿车的利润与该轿车首次出现故障的时间有关．某轿车制造厂生产甲、乙两种品牌轿车，保修期均为2年．现从该厂已售出的两种品牌轿车中各随机抽取50辆，统计数据如下：

    品牌
    		甲
    		 
    		 
    		乙
    		 
    首次出现故障时间x(年)
    		0<x≤1
    		1<x≤2
    		x>2
    		0<x≤2
    		x>2
    轿车数量(辆)
    		2
    		3
    		45
    		5
    		45
    每辆利润(万元)
    		1
    		2
    		3
    		1．8
    		2．9
     
    将频率视为概率，解答下列问题：
    (1)从该厂生产的甲品牌轿车中随机抽取一辆，求其首次出现故障发生在保修期内的概率；
    (2)若该厂生产的轿车均能售出，记生产一辆甲品牌轿车的利润为X1，生产一辆乙品牌轿车的利润为X2，分别求X1，X2的分布列；
    (3)该厂预计今后这两种品牌轿车销量相当，由于资金限制，只能生产其中一种品牌的轿车．若从经济效益的角度考虑，你认为应生产哪种品牌的轿车？说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某中学有A、B、C、D、E五名同学在高三“一检”中的名次依次为1，2，3，4，5名，“二检”中的前5名依然是这五名同学.
    （1）求恰好有两名同学排名不变的概率；
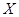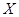    （2）如果设同学排名不变的同学人数为，求的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某学校为了解高三年级学生寒假期间的学习情况，抽取甲、乙两班，调查这两个班的学生在寒假期间每天平均学习的时间（单位：小时），统计结果绘成频率分布直方图（如图）．已知甲、乙两班学生人数相同，甲班学生每天平均学习时间在区间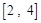的有8人．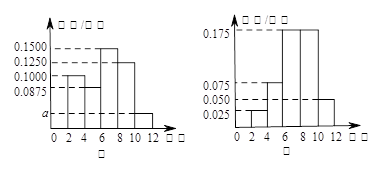

    （1）求直方图中的值及甲班学生每天平均学习时间在区间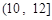的人数；
    （2）从甲、乙两个班每天平均学习时间大于10个小时的学生中任取4人参加测试，设4人中甲班学生的人数为，求的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    袋中装有黑球和白球共7个，从中任取2个球都是白球的概率为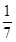，现有甲、乙两人从袋中轮流摸取1球，甲先取，乙后取，然后甲再取，…，取后不放回，直到两人中有一人取到白球时即终止，每个球在每一次被取出的机会是等可能的，用ξ表示取球终止所需要的取球次数．
    (1)求袋中原有白球的个数；
    (2)求随机变量ξ的概率分布；
    (3)求甲取到白球的概率．

    查看答案和解析>>

    同步练习册答案