
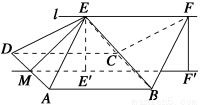
如图,四边形ABCD是边长为2的正方形,直线l与平面ABCD平行,E和F是l上的两个不同点,且EA=ED,FB=FC.E′和F′是平面ABCD内的两点,EE′和FF′都与平面ABCD垂直.

(1)证明:直线E′F′垂直且平分线段AD;
(2)若∠EAD=∠EAB=60 °,EF=2.求多面体ABCDEF的体积.
(1)见解析(2)2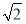 .
.
【解析】(1)证明 ∵EA=ED且EE′⊥平面ABCD,
∴E′D=E′A,∴点E′在线段AD的垂直平分线上.
同理,点F′在线段BC的垂直平分线上.
又四边形ABCD是正方形,
∴线段BC的垂直平分线也就是线段AD的垂直平分线,即点E′、F′都在线段AD的垂直平分线上.
∴直线E′F′垂直且平分线段AD.
(2)解 如图,连接EB、EC,由题意知多面体ABCDEF可分割成正四棱锥E?ABCD和正四面体E?BCF两部分.设AD的中点为M,在Rt△MEE′中,由于ME′=1,ME=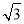 ,∴EE′=
,∴EE′=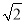 .
.
∴VE?ABCD=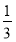 ·S正方形ABCD·EE′=
·S正方形ABCD·EE′=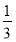 ×22×
×22×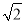 =
=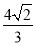 .
.
又VE?BCF=VC?BEF=VC?BEA=VE?ABC= S△ABC·EE′=
S△ABC·EE′=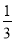 ×
×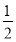 ×22×
×22×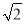 =
=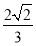 ,
,
∴多面体ABCDEF的体积为VE?ABCD+VE?BCF=2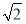 .
.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练18练习卷(解析版) 题型:选择题
设m为正整数,(x+y)2m展开式的二项式系数的最大值为a,(x+y)2m+1展开式的二项式系数的最大值为b,若13a=7b,则m等于( ).
A.5 B.6 C.7 D.8
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:填空题
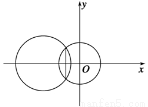
若圆x2+y2=4与圆x2+y2+2ax-6=0(a>0)的公共弦的长为2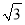 ,则a=________.
,则a=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练12练习卷(解析版) 题型:解答题
如图,在四棱台ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2AD,AD=A1B1,∠BAD=60°.
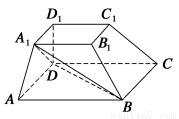
(1)证明:AA1⊥BD;
(2)证明:CC1∥平面A1BD.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练12练习卷(解析版) 题型:选择题
已知两条不同的直线m,n和两个不同的平面α,β,给出下列四个命题:
①若m∥α,n∥β,且α∥β,则m∥n;②若m∥α,n⊥β,且α⊥β,则m∥n;③若m⊥α,n∥β,且α∥β,则m⊥n;④若m⊥α,n⊥β,且α⊥β,则m⊥n.其中正确的个数有( ).
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练11练习卷(解析版) 题型:选择题
在具有如图所示的正视图和俯视图的几何体中,体积最大的几何体的表面积为( ).
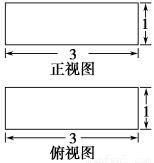
A.13 B.7+3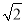 C.
C.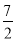 π D.14
π D.14
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练10练习卷(解析版) 题型:解答题
正项数列{an}的前n项和Sn满足: -(n2+n-1)Sn-(n2+n)=0.
-(n2+n-1)Sn-(n2+n)=0.
(1)求数列{an}的通项公式an;
(2)令bn= ,数列{bn}的前n项和为Tn,证明:对于任意的n∈N*,都有Tn<
,数列{bn}的前n项和为Tn,证明:对于任意的n∈N*,都有Tn< .
.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷5练习卷(解析版) 题型:填空题
已知双曲线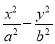 =1(a>0,b>0)的渐近线方程为y=±
=1(a>0,b>0)的渐近线方程为y=±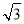 x,则它的离心率为________.
x,则它的离心率为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷2练习卷(解析版) 题型:解答题
在△ABC中,角A,B,C所对的边分别为a,b,c,已知cos C+(cos A-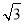 sin A)cos B=0.
sin A)cos B=0.
(1)求角B的大小;
(2)若a+c=1,求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com