若圆x2＋y2＝4与圆x2＋y2＋2ax－6＝0(a＞0)的公共弦的长为2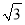
，则a＝________.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练训练8练习卷（解析版） 题型：解答题
A，B分别是单位圆与x轴、y轴正半轴的交点，点P在单位圆上，∠AOP＝θ(0<θ<π)，C点坐标为(－2,0)，平行四边形OAQP的面积为S.
(1)求
·
＋S的最大值；
(2)若CB∥OP，求sin
的值．
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练训练17练习卷（解析版） 题型：选择题
某班级有50名学生，其中有30名男生和20名女生，随机询问了该班五名男生和五名女生在某次数学测验中的成绩，五名男生的成绩分别为86,94,88,92,90，五名女生的成绩分别为88,93,93,88,93.下列说法一定正确的是( )．
A．这种抽样方法是一种分层抽样
B．这种抽样方法是一种系统抽样
C．这五名男生成绩的方差大于这五名女生成绩的方差
D．该班男生成绩的平均数小于该班女生成绩的平均数
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练训练15练习卷（解析版） 题型：填空题
设抛物线y2＝8x的焦点为F，准线为l，P为抛物线上一点PA⊥l，A为垂足，如果AF的斜率为－
，那么|PF|＝________.
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练训练14练习卷（解析版） 题型：解答题
已知以点C
(t∈R，t≠0)为圆心的圆与x轴交于点O，A，与y轴交于点O，B，其中O为原点．
(1)求证：△AOB的面积为定值；
(2)设直线2x＋y－4＝0与圆C交于点M，N，若|OM|＝|ON|，求圆C的方程；
(3)在(2)的条件下，设P，Q分别是直线l：x＋y＋2＝0和圆C上的动点，求|PB|＋|PQ|的最小值及此时点P的坐标．
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练训练14练习卷（解析版） 题型：选择题
已知倾斜角为α的直线l与直线x－2y＋2＝0平行，则tan 2α的值为( )．
A.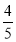
B.
C.
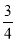D.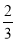
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练训练13练习卷（解析版） 题型：选择题
如图所示，正方体ABCD-A1B1C1D1的棱长为1，线段B1D1上有两个动点E，F且EF＝
，则下列结论中错误的是( )．
A．AC⊥BE
B．EF∥平面ABCD
C．三棱锥A-BEF的体积为定值
D．异面直线AE，BF所成的角为定值
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练训练11练习卷（解析版） 题型：解答题
如图，四边形ABCD是边长为2的正方形，直线l与平面ABCD平行，E和F是l上的两个不同点，且EA＝ED，FB＝FC.E′和F′是平面ABCD内的两点，EE′和FF′都与平面ABCD垂直．
(1)证明：直线E′F′垂直且平分线段AD；
(2)若∠EAD＝∠EAB＝60 °，EF＝2.求多面体ABCDEF的体积．
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练优化重组卷4练习卷（解析版） 题型：解答题
如图，在四棱锥P-ABCD中，PA⊥平面ABCD，E为BD的中点，G为PD的中点，△DAB≌△DCB，EA＝EB＝AB＝1，PA＝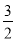
，连接CE并延长交AD于F.
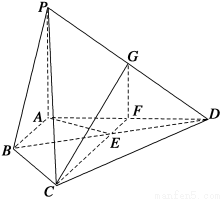
(1)求证：AD⊥平面CFG；
(2)求平面BCP与平面DCP的夹角的余弦值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
