
已知以点C (t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y-4=0与圆C交于点M,N,若|OM|=|ON|,求圆C的方程;
(3)在(2)的条件下,设P,Q分别是直线l:x+y+2=0和圆C上的动点,求|PB|+|PQ|的最小值及此时点P的坐标.
(1)见解析(2)(x-2)2+(y-1)2=5.(3)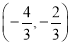
【解析】(1)由题设知,圆C的方程为(x-t)2+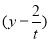 2=t2+
2=t2+ ,化简得x2-2tx+y2-
,化简得x2-2tx+y2- y=0,当y=0时,x=0或2t,则A(2t,0);当x=0时,y=0或
y=0,当y=0时,x=0或2t,则A(2t,0);当x=0时,y=0或 ,则B
,则B ,∴S△AOB=
,∴S△AOB= |OA|·|OB|=
|OA|·|OB|= |2t|·
|2t|· =4为定值.
=4为定值.
(2)∵|OM|=|ON|,则原点O在MN的中垂线上,设MN的中点为H,则CH⊥MN,∴C,H,O三点共线,则直线OC的斜率k= =
= =
= ,∴t=2或t=-2.
,∴t=2或t=-2.
∴圆心为C(2,1)或(-2,-1),∴圆C的方程为(x-2)2+(y-1)2=5或(x+2)2+(y+1)2=5,由于当圆方程为(x+2)2+(y+1)2=5时,直线2x+y-4=0到圆心的距离d>r,此时不满足直线与圆相交,故舍去,∴圆C的方程为(x-2)2+(y-1)2=5.
(3)点B(0,2)关于直线x+y+2=0的对称点为B′(-4,-2),则|PB|+|PQ|=|PB′|+|PQ|≥|B′Q|,又B′到圆上点Q的最短距离为|B′C|-r=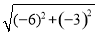 -
-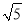 =3
=3 -
-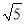 =2
=2 .
.
所以|PB|+|PQ|的最小值为2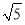 ,直线B′C的方程为y=
,直线B′C的方程为y= x,则直线B′C与直线x+y+2=0的交点P的坐标为
x,则直线B′C与直线x+y+2=0的交点P的坐标为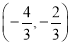 .
.


科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练9练习卷(解析版) 题型:选择题
设等差数列{an}的前n项和为Sn,Sm-1=-2,Sm=0,Sm+1=3,则m等于( ).
A.3 B.4 C.5 D.6
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练17练习卷(解析版) 题型:填空题
在2013年3月15日这天,郑州市物价部门对本市5家商场某商品一天的销售量及其价格进行了调查,5家商场某商品的销售价格x(元)与销售量y(件)之间的一组数据如下表:
价格x | 9 | 9.5 | 10 | 10.5 | 11 |
销售量y | 11 | 10 | 8 | 6 | 5 |
作出散点图,可知销售量y与价格x之间具有线性相关关系,其线性回归方程是 =-3.2x+
=-3.2x+ 则实数
则实数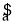 的值是________.
的值是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(解析版) 题型:选择题
若双曲线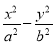 =1(a>0,b>0)与直线y=
=1(a>0,b>0)与直线y=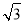 x无交点,则离心率e的取值范围是( ).
x无交点,则离心率e的取值范围是( ).
A.(1,2) B.(1,2] C.(1,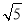 ) D.(1,
) D.(1,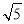 ]
]
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练15练习卷(解析版) 题型:选择题
抛物线C1:y=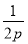 x2(p>0)的焦点与双曲线C2:
x2(p>0)的焦点与双曲线C2: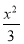 -y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=( ).
-y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=( ).
A. 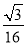 B.
B. 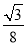 C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:填空题
若圆x2+y2=4与圆x2+y2+2ax-6=0(a>0)的公共弦的长为2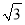 ,则a=________.
,则a=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练13练习卷(解析版) 题型:解答题
在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,且PA⊥平面ABCD.

(1)求证:PC⊥BD;
(2)过直线BD且垂直于直线PC的平面交PC于点E,且三棱锥E-BCD的体积取到最大值.
①求此时四棱锥E-ABCD的高;
②求二面角A-DE-B的正弦值的大小.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练12练习卷(解析版) 题型:选择题
已知两条不同的直线m,n和两个不同的平面α,β,给出下列四个命题:
①若m∥α,n∥β,且α∥β,则m∥n;②若m∥α,n⊥β,且α⊥β,则m∥n;③若m⊥α,n∥β,且α∥β,则m⊥n;④若m⊥α,n⊥β,且α⊥β,则m⊥n.其中正确的个数有( ).
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷5练习卷(解析版) 题型:选择题
圆(x+2)2+y2=4与圆(x-2)2+(y-1)2=9的位置关系为( ).
A.内切 B.相交
C.外切 D.相离
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com