
在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,且PA⊥平面ABCD.

(1)求证:PC⊥BD;
(2)过直线BD且垂直于直线PC的平面交PC于点E,且三棱锥E-BCD的体积取到最大值.
①求此时四棱锥E-ABCD的高;
②求二面角A-DE-B的正弦值的大小.
(1)见解析(2)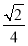 ,
,
【解析】(1)连接AC,因为四边形ABCD是正方形,所以BD⊥AC.因为PA⊥平面ABCD,所以PA⊥BD.
又AC∩PA=A,所以BD⊥平面PAC.
又PC?平面PAC,所以PC⊥BD.
(2)解 ①设PA=x,三棱锥E-BCD的底面积为定值,在△PBC中,易知PB=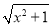 ,PC=
,PC=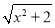 ,
,
又BC=1,故△PBC直角三角形.又BE⊥PC,得EC=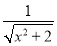 ,可求得该三棱锥的高h=
,可求得该三棱锥的高h=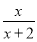 =
=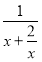 .
.
当且仅当x=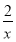 ,即x=
,即x=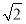 时,三棱锥E-BCD的体积取到最大值,所以h=
时,三棱锥E-BCD的体积取到最大值,所以h=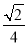 .
.
此时四棱锥E-ABCD的高为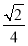 .
.
②以点A为原点,AB,AD,AP所在直线为坐标轴建立空间直角坐标系,则A(0,0,0),C(1,1,0),D(0,1,0),P(0,0,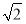 ),易求得CE=
),易求得CE=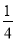 CP.
CP.
所以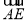 =
=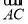 +
+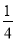
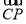 =
= ,
,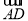 =(0,1,0).
=(0,1,0).
设平面ADE的法向量n1=(x,y,z),则
即 令x=
令x=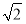 ,则n1=(
,则n1=(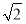 ,0,-3),
,0,-3),
同理可得平面BDE的法向量n2= =(-1,-1,
=(-1,-1,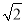 ),所以cos〈n1,n2〉=
),所以cos〈n1,n2〉=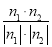 =-
=-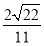 .所以sin〈n1,n2〉=
.所以sin〈n1,n2〉=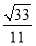 .所以二面角A-DE-B的正弦值的大小为
.所以二面角A-DE-B的正弦值的大小为 .
.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练8练习卷(解析版) 题型:选择题
△ABC中D为BC边的中点,已知 =a,
=a, 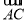 =b则在下列向量中与
=b则在下列向量中与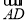 同向的向量是( ).
同向的向量是( ).
A.  B.
B. 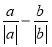 C.
C. 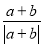 D.|b|a+|a|b
D.|b|a+|a|b
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(解析版) 题型:填空题
抛物线x2=2py(p>0)的焦点为F,其准线与双曲线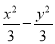 =1相交于A,B两点,若△ABF为等边三角形,则p=________.
=1相交于A,B两点,若△ABF为等边三角形,则p=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:解答题
已知以点C (t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y-4=0与圆C交于点M,N,若|OM|=|ON|,求圆C的方程;
(3)在(2)的条件下,设P,Q分别是直线l:x+y+2=0和圆C上的动点,求|PB|+|PQ|的最小值及此时点P的坐标.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:选择题
已知圆的方程为x2+y2-6x-8y=0,设该圆中过点(3,5)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积是( ).
A.10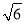 B.20
B.20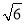 C.30
C.30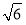 D.40
D.40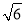
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练13练习卷(解析版) 题型:选择题
如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F且EF= ,则下列结论中错误的是( ).
,则下列结论中错误的是( ).

A.AC⊥BE
B.EF∥平面ABCD
C.三棱锥A-BEF的体积为定值
D.异面直线AE,BF所成的角为定值
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练12练习卷(解析版) 题型:解答题
如图,正方形ABCD和三角形ACE所在的平面互相垂直,EF∥BD,AB= EF.
EF.

(1)求证:BF∥平面ACE;
(2)求证:BF⊥BD.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练11练习卷(解析版) 题型:选择题
某几何体的三视图如图所示,则该几何体的体积为( ).

A.  B.
B.  C.200 D.240
C.200 D.240
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(解析版) 题型:选择题
如图,某几何体的正视图、侧视图、俯视图均为直角三角形,则这个几何体的表面中,直角三角形个数为( ).

A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com