
如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F且EF= ,则下列结论中错误的是( ).
,则下列结论中错误的是( ).

A.AC⊥BE
B.EF∥平面ABCD
C.三棱锥A-BEF的体积为定值
D.异面直线AE,BF所成的角为定值
D
【解析】∵AC⊥平面BB1D1D,又BE?平面BB1D1D.∴AC⊥BE,故A正确.∵B1D1∥平面ABCD,又E,F在直线D1B1上运动,∴EF∥平面ABCD,故B正确.C中,由于点B到直线B1D1的距离不变,故△BEF的面积为定值,又点A到平面BEF的距离为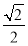 ,故VA-BEF为定值.故C正确.
,故VA-BEF为定值.故C正确.
建立空间直角坐标系,如图所示,可得A(1,1,0),B(0,1,0),
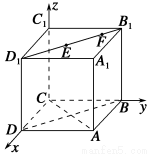
①当点E在D1处,点F为D1B1的中点时,E(1,0,1),F (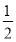 ,
,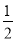 ,1),
,1),
∴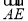 =(0,-1,1),
=(0,-1,1),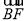 =(
=(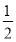 ,-
,-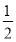 ,1),
,1),
∴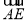 ·
·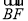 =
=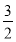 .又|
.又|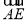 |=
|= ,|
,|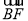 |=
|=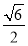 ,
,
∴cos〈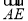 ,
,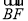 〉=
〉=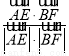 =
=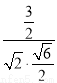 =
=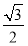 .
.
∴此时异面直线AE与BF成30°角.
②当点E为D1B1的中点,F在B1处,此时E(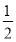 ,
,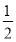 ,1),F(0,1,1),∴
,1),F(0,1,1),∴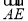 =(-
=(-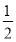 ,-
,-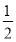 ,1),
,1),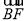 =(0,0,1),
=(0,0,1),
∴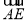 ·
·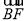 =1,|
=1,|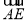 |=
|=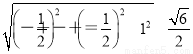 ,∴cos〈
,∴cos〈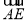 ,
,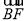 〉=
〉=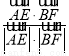 =
= ,故选D.
,故选D.


科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练7练习卷(解析版) 题型:解答题
已知函数f(x)=2cos (其中ω>0,x∈R)的最小正周期为10π.
(其中ω>0,x∈R)的最小正周期为10π.
(1)求ω的值;
(2)设α,β∈ ,f
,f =-
=- ,f
,f =
= ,求cos(α+β)的值.
,求cos(α+β)的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(解析版) 题型:选择题
若双曲线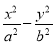 =1(a>0,b>0)与直线y=
=1(a>0,b>0)与直线y=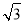 x无交点,则离心率e的取值范围是( ).
x无交点,则离心率e的取值范围是( ).
A.(1,2) B.(1,2] C.(1,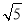 ) D.(1,
) D.(1,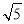 ]
]
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:填空题
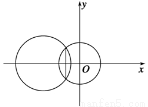
若圆x2+y2=4与圆x2+y2+2ax-6=0(a>0)的公共弦的长为2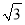 ,则a=________.
,则a=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练13练习卷(解析版) 题型:解答题
在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,且PA⊥平面ABCD.

(1)求证:PC⊥BD;
(2)过直线BD且垂直于直线PC的平面交PC于点E,且三棱锥E-BCD的体积取到最大值.
①求此时四棱锥E-ABCD的高;
②求二面角A-DE-B的正弦值的大小.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练12练习卷(解析版) 题型:解答题
如图,在四棱台ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2AD,AD=A1B1,∠BAD=60°.
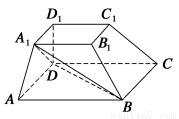
(1)证明:AA1⊥BD;
(2)证明:CC1∥平面A1BD.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练12练习卷(解析版) 题型:选择题
已知两条不同的直线m,n和两个不同的平面α,β,给出下列四个命题:
①若m∥α,n∥β,且α∥β,则m∥n;②若m∥α,n⊥β,且α⊥β,则m∥n;③若m⊥α,n∥β,且α∥β,则m⊥n;④若m⊥α,n⊥β,且α⊥β,则m⊥n.其中正确的个数有( ).
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练10练习卷(解析版) 题型:解答题
正项数列{an}的前n项和Sn满足: -(n2+n-1)Sn-(n2+n)=0.
-(n2+n-1)Sn-(n2+n)=0.
(1)求数列{an}的通项公式an;
(2)令bn= ,数列{bn}的前n项和为Tn,证明:对于任意的n∈N*,都有Tn<
,数列{bn}的前n项和为Tn,证明:对于任意的n∈N*,都有Tn< .
.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(解析版) 题型:解答题
已知函数f(x)= 的图象过原点,且关于点(-1,2)成中心对称.
的图象过原点,且关于点(-1,2)成中心对称.
(1)求函数f(x)的解析式;
(2)若数列{an}满足a1=2,an+1=f(an),试证明数列 为等比数列,并求出数列{an}的通项公式.
为等比数列,并求出数列{an}的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com