
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1,PA=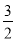 ,连接CE并延长交AD于F.
,连接CE并延长交AD于F.
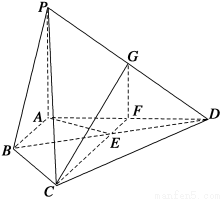
(1)求证:AD⊥平面CFG;
(2)求平面BCP与平面DCP的夹角的余弦值.
(1)见解析(2)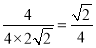
【解析】(1)在△ABD中,因为E是BD中点,所以EA=EB=ED=AB=1,故∠BAD=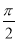 ,∠ABE=∠AEB=
,∠ABE=∠AEB=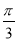 ,
,
因为△DAB≌△DCB,所以△EAB≌△ECB,从而有∠FED=∠BEC=∠AEB=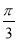 ,
,
所以∠FED=∠FEA.故EF⊥AD,AF=FD,又因为PG=GD,
所以FG∥PA,又PA⊥平面ABCD,所以GF⊥AD,故AD⊥平面CFG.
(2)以A为坐标原点建立如图所示的坐标系,
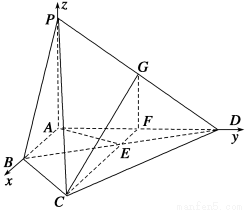
则A(0,0,0),B(1,0,0),C ,D(0,
,D(0,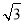 ,0),P
,0),P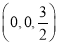 ,故
,故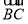 =
= ,
,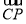 =
= ,
,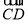 =
= .
.
设平面BCP的法向量n1=(x1,y1,z1),
则
令y1=-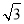 ,则x1=3,z1=2,n1=(3,-
,则x1=3,z1=2,n1=(3,-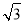 ,2).
,2).
设平面DCP的一个法向量n2=(1,y2,z2),则
解得 即n2=(1,
即n2=(1,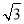 ,2).
,2).
从而平面BCP与平面DCP的夹角θ的余弦值为
cos θ=|cos〈n1,n2〉|=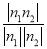 =
=


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:填空题
若圆x2+y2=4与圆x2+y2+2ax-6=0(a>0)的公共弦的长为2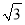 ,则a=________.
,则a=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练10练习卷(解析版) 题型:解答题
正项数列{an}的前n项和Sn满足: -(n2+n-1)Sn-(n2+n)=0.
-(n2+n-1)Sn-(n2+n)=0.
(1)求数列{an}的通项公式an;
(2)令bn= ,数列{bn}的前n项和为Tn,证明:对于任意的n∈N*,都有Tn<
,数列{bn}的前n项和为Tn,证明:对于任意的n∈N*,都有Tn< .
.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷5练习卷(解析版) 题型:填空题
已知双曲线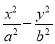 =1(a>0,b>0)的渐近线方程为y=±
=1(a>0,b>0)的渐近线方程为y=±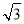 x,则它的离心率为________.
x,则它的离心率为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷5练习卷(解析版) 题型:选择题
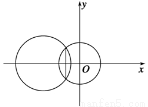
圆(x+2)2+y2=4与圆(x-2)2+(y-1)2=9的位置关系为( ).
A.内切 B.相交
C.外切 D.相离
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(解析版) 题型:解答题
已知函数f(x)= 的图象过原点,且关于点(-1,2)成中心对称.
的图象过原点,且关于点(-1,2)成中心对称.
(1)求函数f(x)的解析式;
(2)若数列{an}满足a1=2,an+1=f(an),试证明数列 为等比数列,并求出数列{an}的通项公式.
为等比数列,并求出数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷2练习卷(解析版) 题型:解答题
在△ABC中,角A,B,C所对的边分别为a,b,c,已知cos C+(cos A-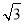 sin A)cos B=0.
sin A)cos B=0.
(1)求角B的大小;
(2)若a+c=1,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练x4-1练习卷(解析版) 题型:填空题
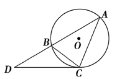
如图,点A、B、C都在⊙O上,过点C的切线交AB的延长线于点D,若AB=5,BC=3,CD=6,则线段AC的长为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com