
【题目】如图,在直角梯形 ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为线段
为线段 ![]() 的中点,将
的中点,将 ![]() 沿
沿 ![]() 折起,使平面
折起,使平面 ![]() 平面
平面 ![]() ,得到几何体
,得到几何体 ![]() .
.
(1)若 ![]() 分别为线段
分别为线段 ![]() 的中点,求证:
的中点,求证: ![]() 平面
平面 ![]() ;
;
(2)求证: ![]() 平面
平面 ![]() ;
;
(3)求 ![]() 的值.
的值.
【答案】
(1)证明:∵折叠前后CD、BG位置关系不改变,
∴CD∥BG.
∵ E、F分别为线段AC、BD的中点,
∴EF∥CD,
∴ EF∥BG.
又EF ![]() 平面ABG,BG平面ABG,
平面ABG,BG平面ABG,
∴ EF∥平面ABG.
(2)证明:∵ 将△ADG沿GD折起后,AG、GD位置关系不改变,
∴AG⊥GD,
又平面ADG⊥平面BCDG,平面ADG∩平面BCDG=GD,AG平面AGD,
∴ AG⊥平面BCDG
(3)由已知得BC=CD=AG=2,
又由(2)得AG⊥平面BCDG,
∴点A到平面BCDG的距离AG=2,
∴ ![]()
【解析】(1)根据中位线定理证明EF//CD,再根据直线与直线平行的性质证明EF//GB,最后根据直线与平面平行的判定定理,证明 EF//平面ABG。
(2)根据平面与平面垂直的性质定理可以证明结论。
(3)利用等体积法,结合三棱锥的体积计算公式求解。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】底面为正方形的四棱锥S﹣ABCD,且SD⊥平面ABCD,SD= ![]() ,AB=1,线段SB上一M点满足
,AB=1,线段SB上一M点满足 ![]() =
= ![]() ,N为线段CD的中点,P为四棱锥S﹣ABCD表面上一点,且DM⊥PN,则点P形成的轨迹的长度为( )
,N为线段CD的中点,P为四棱锥S﹣ABCD表面上一点,且DM⊥PN,则点P形成的轨迹的长度为( )
A.![]()
B.![]()
C.![]()
D.2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某种水箱用的“浮球”,是由两个半球和一个圆柱筒组成的.已知半球的直径是6 cm,圆柱筒高为2 cm.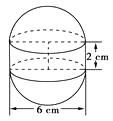
(1)这种“浮球”的体积是多少cm3(结果精确到0.1)?
(2)要在2 500个这样的“浮球”表面涂一层胶,如果每平方米需要涂胶100克,那么共需胶多少克?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ ![]() ﹣3lnx(a∈R).
﹣3lnx(a∈R).
(1)若x=3是f(x)的一个极值点,求a值及f(x)的单调区间;
(2)当a=﹣2时,求f(x)在区间[1,e]上的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为me , 众数为mO , 平均值为 ![]() ,则( )
,则( )
A.me=mO= ![]()
B.me=mO< ![]()
C.me<mO< ![]()
D.mO<me< ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com