Question

【题目】已知直线x﹣2y+2与圆C：x2+y2﹣4y+m=0相交，截得的弦长为
（1）求圆C的方程；
（2）过点M（﹣1，0）作圆C的切线，求切线的直线方程；
（3）若抛物线y=x2上任意三个不同的点P、Q、R，且满足直线PQ和PR都与圆C相切，判断直线QR与圆C的位置关系，并加以证明．

Answer 1

【答案】
（1）解：圆心C（0，2）到直线x﹣2y+2与的距离为d= ，

∵截得的弦长为 ，∴r=1

∴圆C的方程为：x2+（y﹣2）2=1

（2）解：斜率不存在时，x=﹣1满足题意；

斜率存在时，设直线方程为y=k（x+1），即kx﹣y+k=0，

圆心到直线的距离d= =1，∴k=﹣ ，切线方程为3x+4y+3=0，

综上所述，切线方程为x=﹣1或3x+4y+3=0

（3）解：设P（a，a2），Q（b，b2），R（c，c2），可得kPQ=a+b，

直线PQ的方程为y﹣a2=（a+b）（x﹣a），即为y=（a+b）x﹣ab，

同理可得，直线PR的方程为y=（a+c）x﹣ac，

直线QR的方程为y=（b+c）x﹣bc，

∵直线PQ和PR都与圆C相切，

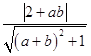∴ =1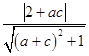， =1，即为b2（1﹣a2）﹣2ab+a2﹣3=0，

c2（1﹣a2）﹣2ac+a2﹣3=0，即有b，c为方程x2（1﹣a2）﹣2ax+a2﹣3=0的两根，

可得b+c= ，bc= ，

由圆心到直线QR的距离为 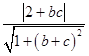=1，

则直线QR与圆C相切

【解析】（1）求得圆心到直线的距离，由弦长公式，计算即可得到m=3，进而得到圆的方程；（2）分类讨论，运用直线和圆相切的条件，求得k，即可得出结论；（3）设P（a，a2），Q（b，b2），R（c，c2），求得直线PQ，PR，QR的方程，运用直线和圆相切的条件，化简整理，再由韦达定理，可得b，c的关系，再由圆心到直线QR的距离，即可判断所求位置关系．