
【题目】用黑白两种颜色随机地染如图所示表格中6个格子,每格子染一种颜色,并且从左往右数,不管数到哪个格子,总有黑色格子不少于白色格子的染色方法种数为________.
![]()
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
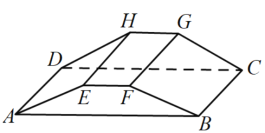
【题目】我国古代《九章算术》中将上,下两面为平行矩形的六面体称为刍童.如图的刍童![]() 有外接球,且
有外接球,且![]() ,
,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 与平面
与平面![]() 间的距离为
间的距离为![]() ,则该刍童外接球的体积为( )
,则该刍童外接球的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
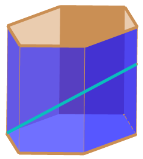
【题目】在我国瓷器的历史上六棱形的瓷器非常常见,因为六、八是中国人的吉利数字,所以好多瓷器都做成六棱形和八棱形.数学李老师有一个正六棱柱形状的笔筒,如图,底面边长为![]() ,高为
,高为![]() (底部及筒壁厚度忽略不计).一根长度为
(底部及筒壁厚度忽略不计).一根长度为![]() 的圆铁棒
的圆铁棒![]() (粗细忽略不计)斜放在笔筒内部,
(粗细忽略不计)斜放在笔筒内部,![]() 的一端置于正六棱柱某一侧棱的底端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为______
的一端置于正六棱柱某一侧棱的底端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为______![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
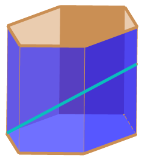
【题目】在我国瓷器的历史上六棱形的瓷器非常常见,因为六、八是中国人的吉利数字,所以好多瓷器都做成六棱形和八棱形.数学李老师有一个正六棱柱形状的笔筒,如图,底面边长为![]() ,高为
,高为![]() (底部及筒壁厚度忽略不计).一根长度为
(底部及筒壁厚度忽略不计).一根长度为![]() 的圆铁棒
的圆铁棒![]() (粗细忽略不计)斜放在笔筒内部,
(粗细忽略不计)斜放在笔筒内部,![]() 的一端置于正六棱柱某一侧棱的底端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为______
的一端置于正六棱柱某一侧棱的底端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为______![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点
的中心在原点![]() ,焦点在
,焦点在![]() 轴上,左右焦点分别为
轴上,左右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,右焦点到右顶点的距离为1.
,右焦点到右顶点的距离为1.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,则
,则![]() 的面积是否存在最大值?若存在,求出这个最大值及直线
的面积是否存在最大值?若存在,求出这个最大值及直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com