
从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如下:
(Ⅰ)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
(Ⅱ)以上述样本的频率作为概率,从该校高三学生中有放回地抽取3人,记抽取的学生成绩不低于90分的人数为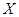 ,求
,求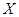 的分布列和期望.
的分布列和期望.
(Ⅰ)92分;(Ⅱ)分布列详见解析,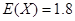 .
.
解析试题分析:本题主要考查频率分布直方图的读图能力和计算能力,以及离散型随机变量的分布列与数学期望.第一问根据频率分布直方图,求该校高三学生本次数学考试的平均分,解决实际问题,公式为:每一个区间的中点×每一个长方形的高×组距,把所得结果相加即可;第二问利用频率=高×组距,求出样本中成绩不低于90分的频率,通过分析发现人数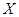 符合二项分布,利用二项分布的概率计算公式:
符合二项分布,利用二项分布的概率计算公式: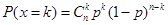 来计算每种情况的概率,列出分布列,由于
来计算每种情况的概率,列出分布列,由于 ,所以利用上面的公式计算期望.
,所以利用上面的公式计算期望.
试题解析:(Ⅰ)由频率分布直方图,得该校高三学生本次数学考试的平均分为 5分
5分
(Ⅱ)样本中成绩不低于90分的频率为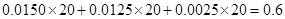 ,
,
所以从该校高三学生中随机抽取1人,分数不低于90分的概率为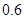 . 7分
. 7分
由题意,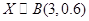 ,
, (
( ),
),
其概率分布列为:
10分X 0 1 2 3 P 0.064 0.288 0.432 0.216  的期望为
的期望为 .
.
考点:1.频率分布直方图;2.分布列;3.数学期望.


科目:高中数学 来源: 题型:解答题
某学校900名学生在一次百米测试中,成绩全部介于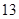 秒与
秒与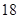 秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组
秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组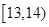 ,第二组
,第二组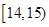 ,…,第五组
,…,第五组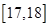 ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.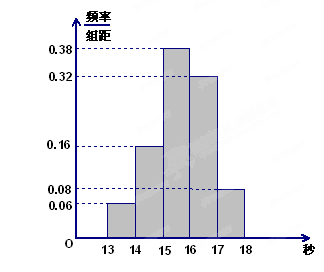
(1)若成绩小于14秒认为优秀,求该样本在这次百米测试中成绩优秀的人数;
(2)请估计学校900名学生中,成绩属于第四组的人数;
(3)请根据频率分布直方图,求样本数据的众数和中位数(保留两位小数).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某种产品的广告费支出 与销售额
与销售额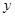 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
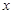 | 2 | 4 | 5 | 6 | 8 |
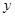 | 30 | 40 | 60 | 50 | 70 |
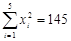


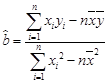 ,
, )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
了解某市今年初二年级男生的身体素质状况,从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试.成绩低于6米为不合格,成绩在6至8米(含6米不含8米)的为及格,成绩在8米至12米(含8米和12米,假定该市初二学生掷实心球均不超过12米)为优秀.把获得的所有数据,分成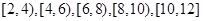 五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
(Ⅰ)求实数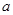 的值及参加“掷实心球”项目测试的人数;
的值及参加“掷实心球”项目测试的人数;
(Ⅱ)根据此次测试成绩的结果,试估计从该市初二年级男生中任意选取一人,“掷实心球”成绩为优秀
的概率;
(Ⅲ)若从此次测试成绩最好和最差的两组男生中随机抽取2名学生再进行其它项目的测试,求所抽取的2名学生来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150) | 总计 |
| 频数 | | | | b | | |
| 频率 | a | 0.25 | | | | |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取的20名学生的成绩进行分析,分数用茎叶图记录如下: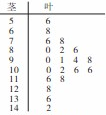
得到频率分步表如下:
(1)求表中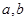 的值,并估计这次考试全校学生数学成绩及格率(分数在
的值,并估计这次考试全校学生数学成绩及格率(分数在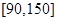 范围为及格);
范围为及格);
(2)从大于等于110分的学生中随机选2名学生得分,求2名学生的平均得分大于等于130分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2013年2月20日,针对房价过高,国务院常务会议确定五条措施(简称“国五条”).为此,记者对某城市的工薪阶层关于“国五条”态度进行了调查,随机抽取了60人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如下表):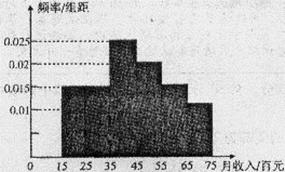
| 月收入(百元) | 赞成人数 |
| [15,25) | 8 |
| [25,35) | 7 |
| [35,45) | 10 |
| [45,55) | 6 |
| [55,65) | 2 |
| [65,75) | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.
(1)如果X=8,求乙组同学植树棵数的平均数和方差;
(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.
(注:方差s2=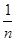 [(x1-
[(x1- )2+(x2-
)2+(x2- )2+…+(xn-
)2+…+(xn- )2]),其中
)2]),其中 为x1,x2,…,xn的平均数)
为x1,x2,…,xn的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2012年元旦、春节前夕,各个物流公司都出现了爆仓现象,直接原因就是网上疯狂的购物.某商家针对人们在网上购物的态度在某城市进行了一次调查,共调查了124人,其中女性70人,男性54人.女性中有43人对网上购物持赞成态度,另外27人持反对态度;男性中有21人赞成网上购物,另外33人持反对态度.
(Ⅰ) 估计该地区对网上购物持赞成态度的比例;
(Ⅱ) 有多大的把握认为该地区对网上购物持赞成态度与性别有关;
附:表1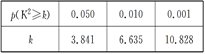
K2=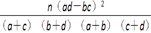
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com