
以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.
(1)如果X=8,求乙组同学植树棵数的平均数和方差;
(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.
(注:方差s2=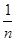 [(x1-
[(x1- )2+(x2-
)2+(x2- )2+…+(xn-
)2+…+(xn- )2]),其中
)2]),其中 为x1,x2,…,xn的平均数)
为x1,x2,…,xn的平均数)
(1) .(2) P(C)=
.(2) P(C)= =
= .
.
解析试题分析:(1)当X=8时,由茎叶图可知,乙组同学的植树棵数是:8,8,9,10,所以平均数为 =
= =
=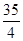 ;
;
方差为s2= [(8-
[(8-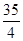 )2+(8-
)2+(8-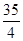 )2+(9-
)2+(9-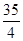 )2+(10-
)2+(10-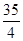 )2]=
)2]= .
.
(2)记甲组四名同学为A1,A2,A3,A4,他们植树的依次为9,9,11,11;乙组四名同学为B1,B2,B3,B4,他们植树的棵数依次为9,8,9,10.分别从甲、乙两组中随机选取一名同学,所有可能的结果有16个,它们是:
(A1,B1),(A1,B2),(A1,B3),(A1,B4),
(A2,B1),(A2,B2),(A2,B3),(A2,B4),
(A3,B1),(A3,B2),(A3,B3),(A3,B4),
(A4,B1),(A4,B2),(A4,B3),(A4,B4),
用C表示:“选出的两名同学的植树总棵数为19”这一事件,则C中的结果有4个,它们是:(A1,B4),(A2,B4),(A3,B2),(A4,B2).故所求概率为P(C)= =
= .
.
考点:茎叶图,平均数,古典概型概率的计算
点评:中档题,古典概型要求所有结果出现的可能性都相等,强调所有结果中每一结果出现的概率都相同.解决问题的步骤是:计算满足条件的基本事件个数,及基本事件的总个数,然后代入古典概型计算公式进行求解。为防止遗漏,常常利用“树图法”或“坐标法”。 茎叶图的优点保留了原始数据,便于统计、记录。


科目:高中数学 来源: 题型:解答题
(本题满分12分)成都市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰。若现有500人参加测试,学生成绩的频率分布直方图如下:
(I)求获得参赛资格的人数;
(II)根据频率直方图,估算这500名学生测试的平均成绩;
(III)若知识竞赛分初赛和复赛,在初赛中每人最多有3次选题答题的机会,累计答对2题或答错2题即终止,答对2题者方可参加复赛,已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响,已知他连续两次答错的概率为 ,求甲通过初赛的概率.
,求甲通过初赛的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如下:
(Ⅰ)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
(Ⅱ)以上述样本的频率作为概率,从该校高三学生中有放回地抽取3人,记抽取的学生成绩不低于90分的人数为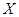 ,求
,求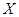 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学举行了一次“环保知识竞赛”, 全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图 所示)解决下列问题:
所示)解决下列问题:
频率分布表
| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 8 | 0.16 |
| 第2组 | [60,70) | a | ▓ |
| 第3组 | [70,80) | 20 | 0.40 |
| 第4组 | [80,90) | ▓ | 0.08 |
| 第5组 | [90,100] | 2 | b |
| | 合计 | ▓ | ▓ |
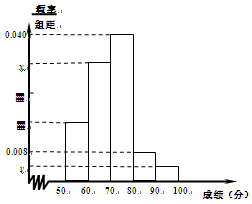
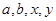 的值;
的值;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校从参加市联考的甲、乙两班数学成绩110分以上的同学中各随机抽取8人,将这16人的数学成绩编成如下茎叶图.
(Ⅰ)茎叶图中有一个数据污损不清(用△表示),若甲班抽出来的同学平均成绩为122分,试推算这个污损的数据是多少?
(Ⅱ)现要从成绩在130分以上的5位同学中选2位作数学学习方法介绍,请将所有可能的结果列举出来,并求选出的两位同学不在同一个班的概率. 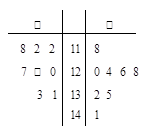
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一次考试中,五名学生的数学、物理成绩如下表所示: 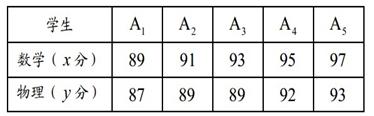
(1)要从 5 名学生中选2 人参加一项活动,求选中的学生中至少有一人的物理成绩高于90分的概率;
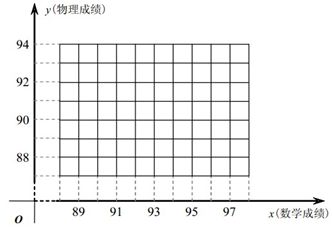
(2)请在所给的直角坐标系中画出它们的散点图,并求这些数据的线性回归方程  .
.
(附:回归直线的方程是 :  , 其中
, 其中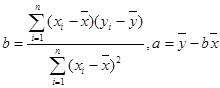 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
公安部最新修订的《机动车驾驶证申领和使用的规定》于2013年1月1日起正式实施,新规实施后,获取驾照要经过三个科目的考试,先考科目一(理论一),科目一过关后才能再考科目二(桩考和路考),科目二过关后还要考科目三(理论二),只有三个科目都过关后才能拿到驾驶证,某驾校现有100名新学员,第一批参加的20人各科目通过的人数情况如下表:
| 参考人数 | 通过科目一人数 | 通过科目二人数 | 通过科目三人数 |
| 20 | 12 | 4 | 2 |
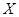 为学校因为该学员而奖励教官的金额数,求
为学校因为该学员而奖励教官的金额数,求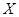 的数学期望。
的数学期望。查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100棵种子中的发芽数,得到如下资料:
| 日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
| 温差x(℃) | 10 | 11 | 13 | 12 | 8 |
| 发芽y(颗) | 23 | 25 | 30 | 26 | 16 |

 ,
, 

 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com