
一次考试中,五名学生的数学、物理成绩如下表所示: 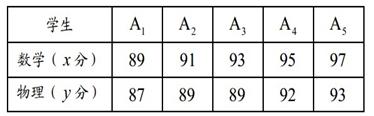
(1)要从 5 名学生中选2 人参加一项活动,求选中的学生中至少有一人的物理成绩高于90分的概率;
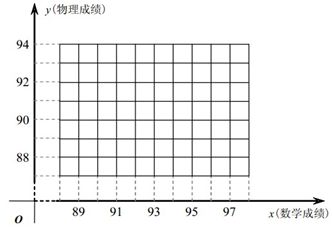
(2)请在所给的直角坐标系中画出它们的散点图,并求这些数据的线性回归方程  .
.
(附:回归直线的方程是 :  , 其中
, 其中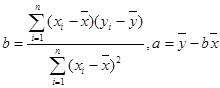 )
)
科目:高中数学 来源: 题型:解答题
某种产品的广告费支出 与销售额
与销售额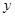 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
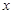 | 2 | 4 | 5 | 6 | 8 |
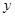 | 30 | 40 | 60 | 50 | 70 |
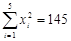


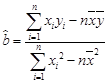 ,
, )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2013年2月20日,针对房价过高,国务院常务会议确定五条措施(简称“国五条”).为此,记者对某城市的工薪阶层关于“国五条”态度进行了调查,随机抽取了60人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如下表):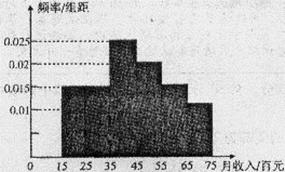
| 月收入(百元) | 赞成人数 |
| [15,25) | 8 |
| [25,35) | 7 |
| [35,45) | 10 |
| [45,55) | 6 |
| [55,65) | 2 |
| [65,75) | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.
(1)如果X=8,求乙组同学植树棵数的平均数和方差;
(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.
(注:方差s2=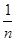 [(x1-
[(x1- )2+(x2-
)2+(x2- )2+…+(xn-
)2+…+(xn- )2]),其中
)2]),其中 为x1,x2,…,xn的平均数)
为x1,x2,…,xn的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了研究玉米品种对产量的影响,某农科院对一块试验田种植的一批玉米共10000 株的生长情况进行研究,现采用分层抽样方法抽取50株作为样本,统计结果如下:
| | 高茎 | 矮茎 | 合计 |
| 圆粒 | 11 | 19 | 30 |
| 皱粒 | 13 | 7 | 20 |
| 合计 | 24 | 26 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
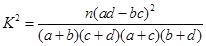 ,其中
,其中 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
给出施化肥量(kg)对水稻产量(kg)影响的试验数据:
| 施化肥量x | 15 | 20 | 25 | 30 |
| 水稻产量y | 330 | 345 | 365 | 405 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2012年元旦、春节前夕,各个物流公司都出现了爆仓现象,直接原因就是网上疯狂的购物.某商家针对人们在网上购物的态度在某城市进行了一次调查,共调查了124人,其中女性70人,男性54人.女性中有43人对网上购物持赞成态度,另外27人持反对态度;男性中有21人赞成网上购物,另外33人持反对态度.
(Ⅰ) 估计该地区对网上购物持赞成态度的比例;
(Ⅱ) 有多大的把握认为该地区对网上购物持赞成态度与性别有关;
附:表1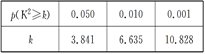
K2=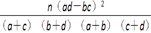
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某重点中学的高二英语老师Vivien,为调查学生的单词记忆时间开展问卷调查。发现在回收上来的1000份有效问卷中,有600名同学们背英语单词的时间安排在白天,另外400名学生晚上临睡前背。Vivien老师用分层抽样的方法抽取50名学生进行实验,实验方法是使两组学生记忆40个无意义音节(如XIQ、GEH),均要求在刚能全部记清时就停止识记,并在8小时后进行记忆测验。不同的是,甲组同学识记结束后一直不睡觉,8小时后测验;乙组同学识记停止后立刻睡觉,8小时后叫醒测验。
乙组同学识记停止8小时后的准确回忆(保持)情况如图。
(1)由分层抽样方法,抽取的50名学生乙组应有几名?
(2)从乙组准确回忆音节数在[8,20)范围内的学生中随机选2人,求两人均准确回忆12个(含12个)以上的概率;
(3)若从是否睡前记忆单词和单词小测能否优秀进行统计,运用2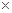 2列联表进行独立性检验,经计算K2=4.069,参考下表你能得到什么统计学结论?
2列联表进行独立性检验,经计算K2=4.069,参考下表你能得到什么统计学结论?
P(K ≥k0) ≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com