
 上,AB、AC分别过两个焦点F1、F2,当
上,AB、AC分别过两个焦点F1、F2,当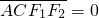 时,有
时,有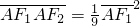 成立.
成立.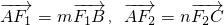 .当点A在椭圆上运动时,求证m+n始终是定值.
.当点A在椭圆上运动时,求证m+n始终是定值.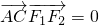 时,
时,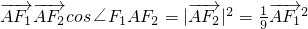 74
74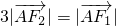 .
.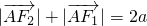 ,
,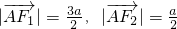 .
.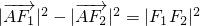 ,
,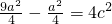 .∴
.∴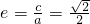 .
. ,得
,得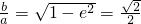 ,∴b=c.
,∴b=c.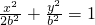 ,即x2+2y2=2b2.
,即x2+2y2=2b2.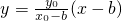 .
.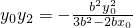 ,则
,则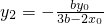 .
.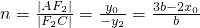 .
.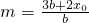 .
.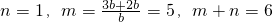 .
.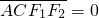 时,有
时,有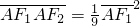 成立,以及椭圆定义,即可得到.
成立,以及椭圆定义,即可得到.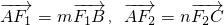 ,分别用参数的式子表示m,n,计算m+n,消去参数,可得一定值,问题得证.
,分别用参数的式子表示m,n,计算m+n,消去参数,可得一定值,问题得证.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
. |
| AC |
. |
| F1F2 |
. |
| AF1 |
. |
| AF2 |
| 1 |
| 9 |
. |
| AF1 |
| AF1 |
| F1B |
| AF2 |
| F2C |
查看答案和解析>>
科目:高中数学 来源:2008年广东地区数学科全国各地模拟试题直线与圆锥曲线大题集 题型:044
已知点A,B,C都在椭圆![]() 上,AB、AC分别过两个焦点F1、F2,当
上,AB、AC分别过两个焦点F1、F2,当![]() 时,有
时,有![]() 成立.
成立.
(1)求此椭圆的离心率;
(2)设![]() .当点A在椭圆上运动时,求证m+n始终是定值.
.当点A在椭圆上运动时,求证m+n始终是定值.
查看答案和解析>>
科目:高中数学 来源:无锡二模 题型:解答题
| x2 |
| a2 |
| y2 |
| b2 |
| . |
| AC |
| . |
| F1F2 |
| . |
| AF1 |
| . |
| AF2 |
| 1 |
| 9 |
| . |
| AF1 |
| AF1 |
| F1B |
| AF2 |
| F2C |
查看答案和解析>>
科目:高中数学 来源:2007年江苏省苏锡常镇四市高考数学二模试卷(解析版) 题型:解答题
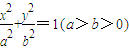 上,AB、AC分别过两个焦点F1、F2,当
上,AB、AC分别过两个焦点F1、F2,当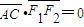 时,有
时,有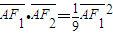 成立.
成立.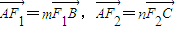 .当点A在椭圆上运动时,求证m+n始终是定值.
.当点A在椭圆上运动时,求证m+n始终是定值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com