练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．某工厂接到一任务，需加工6000个P型零件和2000个Q型零件．这个厂有214名工人，他们每一个人用以加工5个P型零件的时间可以加工3个Q型零件，将这些工人分成两组同时工作，每组加工一种型号的零件．为了在最短时间内完成这批任务，则加工P型零件的人数为137人．

    分析 设最短加工时间为x，建立方程关系进行求解即可．

    解答 解：设最短加工时间为x，
    则加工P型零件的人数为$\frac{6000}{5x}$=$\frac{1200}{x}$，则加工Q型零件的人数为$\frac{2000}{3x}$，
    则满足$\frac{1200}{x}$+$\frac{2000}{3x}$=214，
    即$\frac{3600+2000}{3x}$=214，
    即$\frac{5600}{3x}$=214，
    则$\frac{1}{x}$=$\frac{642}{5600}$，
    则加工P型零件的人数为$\frac{1200}{x}$=1200×$\frac{642}{5600}$=137.57，
    故加工P型零件的人数为137人，
    故答案为：137

    点评 本题主要考查函数的应用问题，根据条件设出变量，建立方程关系是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    20．若2x-2-x=2$\sqrt{3}$，则2x+2-x=4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知四边形ABCD是平行四边形，对角线相交于点O，则下列等式中成立的是（　　）
    A．$\overrightarrow{BC}$+$\overrightarrow{BA}$=$\overrightarrow{AC}$B．$\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$C．$\overrightarrow{AO}$=$\frac{1}{2}$（$\overrightarrow{AB}$+$\overrightarrow{AD}$）D．$\overrightarrow{AD}$=$\overrightarrow{CB}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

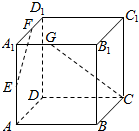    7．如图，在正方体ABCD-A1B1C1D1中，E、F、G分别是AA1，A1D1，A1B1的中点，则异面直线EF与CG所成的角等于（　　）
    A．30°B．45°C．60°D．90°

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．某地区要建造一条防洪堤，其横断面为等腰梯形，腰与底边所成角为60°（如图所示），考虑到防洪堤的坚固性及石块用料等因素，设计其横断面要求面积为9$\sqrt{3}$m2，且髙度不低于$\sqrt{3}$m．问防洪堤横断面的腰长AB为多少时，横断面的外周长AB+BC+CD最小，并求最小外周长：

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知圆C：x2+y2-4x-5=0．
    （Ⅰ）判断圆C与圆D：（x-5）2+（y-4）2=4的位置关系，并说明理由；
    （Ⅱ）若过点（5，4）的直线l与圆C相切，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．阅读下面程序．

    若a=4，则输出的结果是16．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．f （x）是定义在R上的以2为周期的奇函数，f （3）=0，则函数y=f （x）在区间（-2，5）内的零点个数为（　　）
    A．6B．5C．4D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．在△ABC中内角A、B、C所对边分别是a、b、c，若sin2$\frac{B}{2}$=$\frac{c-a}{2c}$，△ABC的形状一定是直角三角形．

    查看答案和解析>>

    同步练习册答案