
(本小题满分12分)如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,PA=2,∠PDA= ,点E、F分别为棱AB、PD的中点.
,点E、F分别为棱AB、PD的中点.

(1)求证:AF∥平面PCE;
(2)求证:平面PCE⊥平面PCD.
(1)见解析;(2)见解析.
【解析】
试题分析:(Ⅰ)利用判定定理证明线面平行时,关键是在平面内找一条与已知直线平行的直线,解题时可先直观判断平面内是否已有,若没有,则需作出该直线,常考虑三角形的中位线、平行四边形的对边或过平行线分线段成比例等.(Ⅱ)证明面面垂直需转化证线面垂直;证明直线和平面垂直的常用方法(1)利用判定定理.(2)利用判定定理的推论(a∥b,a⊥α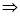 b⊥α).(3)利用面面平行的性质(a⊥α,α∥β
b⊥α).(3)利用面面平行的性质(a⊥α,α∥β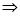 a⊥β).(4)利用面面垂直的性质.
a⊥β).(4)利用面面垂直的性质.
试题解析:(1)取PC的中点G,连结FG、EG
∴FG为△CDP的中位线 ∴FG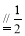 CD
CD
∵四边形ABCD为矩形,E为AB的中点
∴AB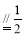 CD ∴FG
CD ∴FG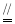 AE ∴四边形AEGF是平行四边形 ∴AF∥EG
AE ∴四边形AEGF是平行四边形 ∴AF∥EG
又EG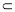 平面PCE,AF
平面PCE,AF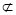 平面PCE ∴AF∥平面. 4分
平面PCE ∴AF∥平面. 4分
(2)∵ PA⊥底面ABCD
∴PA⊥AD,PA⊥CD,又AD⊥CD,PA AD=A
AD=A
∴CD⊥平面ADP 又AF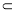 平面ADP ∴CD⊥AF 8分
平面ADP ∴CD⊥AF 8分
直角三角形PAD中,∠PDA=45°
∴△PAD为等腰直角三角形 ∴PA=AD=2
∵F是PD的中点 ∴AF⊥PD,又CD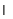 PD=D∴AF⊥平面PCD
PD=D∴AF⊥平面PCD
∵AF∥EG ∴EG⊥平面PCD 又EG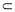 平面PCE
平面PCE
平面PCE⊥平面PCD 12分
考点:立体几何


 考前必练系列答案
考前必练系列答案科目:高中数学 来源:2014-2015学年山东省枣庄市高三1月月考文科数学试卷(解析版) 题型:选择题
若圆C经过(1,0),(3,0)两点,且与y轴相切,则圆C的方程为( )
(A)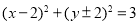
(B)
(C)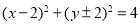
(D)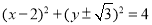
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省枣庄市高三1月月考理科数学试卷(解析版) 题型:选择题
已知定义域为R的函数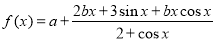 (a、b∈R)有最大值和最小值,且最大值与最小值的和为6,则3a-2b= ( )
(a、b∈R)有最大值和最小值,且最大值与最小值的和为6,则3a-2b= ( )
A. 7 B. 8 C. 9 D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com