考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)连接A1C1,证明AC1⊥B1D1.AC1⊥B1E,利用直线与平面垂直的判定定理证明AC1⊥平面EB1D1;
(2)取B1D1中点O,连C1O,EO,说明∠C1OE为二面角E-B1D1-C1的平面角,通过解三角形即可求解二面角E-B1D1-C1的正切值.
解答:
(本题满分12分)第(1)小题(6分),第(2)小题(6分).
解:(1)证明:连接A
1C
1,由条件得A
1B
1C
1D
1是正方形,因此B
1D
1⊥A
1C
1,
又AA
1⊥平面A
1B
1C
1D
1,所以AA
1⊥B
1D
1,因此B
1D
1⊥平面AA
1C
1,
所以AC
1⊥B
1D
1.同理可证:AC
1⊥B
1E.B
1D
1∩B
1E=B
1,
所以AC
1⊥平面EB
1D
1.
(本题可直接用三垂线定理证明,也可以用建立空间直角坐标系证明,请对照给分)
(2)取B
1D
1中点O,连C
1O,EO,显然C
1O⊥B
1D
1,EO,⊥B
1D
1,∴∠C
1OE为二面角E-B
1D
1-C
1的平面角.
可求
C1O=,C1E=,∵∠EC
1O=90°,∴
tan∠C1OE===.
(若用建立空间直角坐标系,利用向量计算二面角,请对照给分)
点评:本题考查直线与平面垂直的判定定理的应用,二面角的平面角的求法,考查空间想象能力以及计算能力.

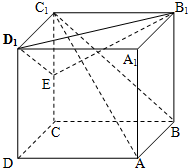 如图,已知长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连结BC1,过点B1作BC1的垂线交CC1于E.
如图,已知长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连结BC1,过点B1作BC1的垂线交CC1于E.

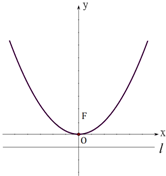 如图,抛物线C的顶点为坐标原点O,焦点F在y轴上,准线l与圆x2+y2=1相切.
如图,抛物线C的顶点为坐标原点O,焦点F在y轴上,准线l与圆x2+y2=1相切.