
已知数列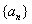 的前
的前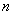 项和为
项和为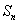 ,且
,且 .(Ⅰ)求数列
.(Ⅰ)求数列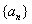 的通项公式;
的通项公式;
(Ⅱ)设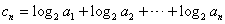 ,
,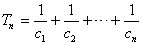 ,求使
,求使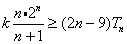 恒成立的实数
恒成立的实数 的取值范围.
的取值范围.
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:
)对于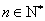 ,将
,将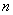 表示为
表示为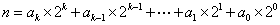 ,当
,当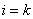 时
时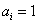 ,当
,当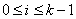 时
时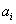 为0或1,定义
为0或1,定义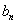 如下:在
如下:在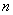 的上述表示中,当
的上述表示中,当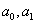 ,
,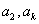 中等于1的个数为奇数时,
中等于1的个数为奇数时,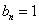 ;否则
;否则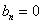 。
。
(1)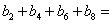 _ _;(2)记
_ _;(2)记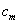 为数列
为数列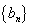 中第
中第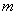 个为0的项与第
个为0的项与第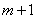 个为0的项之间的项数,则
个为0的项之间的项数,则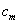 的最大值是___.
的最大值是___.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列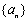 满足:
满足: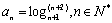 ,我们把使a1· a2·…·ak为整数的数k(
,我们把使a1· a2·…·ak为整数的数k(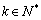 )叫做数列
)叫做数列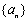 的理想数,给出下列关于数列
的理想数,给出下列关于数列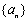 的几个结论:①数列
的几个结论:①数列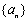 的最小理想数是2;②数列
的最小理想数是2;②数列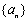 的理想数k的形式可以表示为
的理想数k的形式可以表示为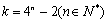 ;③在区间(1,1000)内数列
;③在区间(1,1000)内数列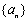 的所有理想数之和为1004;④对任意
的所有理想数之和为1004;④对任意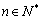 ,有
,有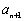 >
>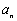 。其中正确结论的序号为 。
。其中正确结论的序号为 。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知首项为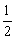 的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.
的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.
(Ⅰ)求数列{an}的通项公式; (Ⅱ)已知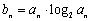 ,求数列{bn}的前n项和
,求数列{bn}的前n项和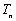 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
在数列{an}中,如果存在非零常数T,使得am+T=am对于任意的非零自然数m均成立,那么就称数列{an}为周期数列,其中T叫数列{an}的周期.已知数列{xn}满足xn+1=|xn-xn-1|(n≥2,n∈N),如果x1=1,x2=a(a∈R,a≠0),当数列{xn}的周期最小时,该数列前2005项的和是( ) A.668 B.669 C.1336 D.1337
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}的通项公式为an=2n+1,令bn=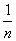 (a1+a2+…+an),则数列{bn}的前10项和T10=( )
(a1+a2+…+an),则数列{bn}的前10项和T10=( )
A.70 B.75C.80 D.85
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com