Question

利用定积分的定义求直线x=1,x=2,y=0和曲线y=x³围成的图形的面积.

Answer 1

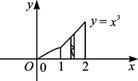
解析：(1)分割将求面积的曲边梯形ABCD分割成n个小曲边梯形，用分点,,…,

将区间［1,2］等分成n个小区间,如图所示,［1,］,［,］,…,［,］,…,［,2］,每个区间的长度为Δx=-=，过各分点作x轴的垂线，把曲边梯形ABCD分割成n个小曲边梯形，它们的面积分别记作ΔS₁，ΔS₂，…，ΔS_n.

(2)近似代替

    取各小区间的左端点记为ε_i，用以点ε_i的纵坐标(ε_i)³为一边，以小区间长Δx=为其邻边的小矩形面积代替第i个小曲边梯形的面积，可近似地表示为ΔS_i≈ε³_i·Δx=()³· (i=1,2,…,n).

(3)作和

    因为每小矩形的面积都可以作为相应的小曲边梯形面积的近似值，所以n个小矩形面积的和就是曲边梯形ABCD面积S的近似值，即S=≈·Δx=·               ①

(4)求极限

    当分点数目越多，即Δx越小，和式①的值就越接近于曲边梯形ABCD的面积S，因此,当n→∞即Δx→0时，和式①的极限就是所求的曲边梯形ABCD的面积.

∴·=

=

=［n(n-1)³+3(n-1)²·+3(n-1)·n(n+1)(2n+1)+n²(n+1)²］.

∴S=·=1++1+=.