
科目:高中数学 来源: 题型:填空题
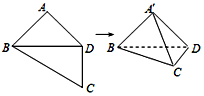 如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(3).
如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(3).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 井号I | 1 | 2 | 3 | 4 | 5 | 6 |
| 坐标(x,y)(km) | (2,30) | (4,40) | (5,60) | (6,50) | (8,70) | (1,y) |
| 钻探深度(km) | 2 | 4 | 5 | 6 | 8 | 10 |
| 出油量(L) | 40 | 70 | 110 | 90 | 160 | 205 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36 | B. | 39 | C. | 312 | D. | 315 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 双曲线x2-y2=1 | B. | 双曲线x2-y2=1的右支 | ||
| C. | 半圆x2+y2=1(x<0) | D. | 一段圆弧x2+y2=1(x>$\frac{{\sqrt{2}}}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com