
设二次函数![]() 满足下列两个条件:
满足下列两个条件:
①当![]() 时,
时,![]() 的最小值为0,且
的最小值为0,且![]() 成立;
成立;
②当![]() 时,
时,![]() ≤
≤![]() 恒成立.
恒成立.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式;
的解析式;
(3)求最大的实数![]() (
(![]() ),使得存在实数
),使得存在实数![]() ,当
,当![]() 时,有
时,有![]() 恒成立.
恒成立.
(1) ![]() (2)
(2) ![]()
(3) 存在t=-4 ,对任意的x∈[1,9] 恒有g(x)≤0, ∴m的最大值为9
(1)在②中令![]() ,有
,有![]() ,故
,故![]() …………………….3分
…………………….3分
(2)由①知二次函数的关于直线![]() 对称,且开口向上………..4分
对称,且开口向上………..4分
故设此二次函数为![]() ,(
,(![]() ),…………………6分
),…………………6分
∵![]() ,∴
,∴![]() ……………………………………….……….7分
……………………………………….……….7分
∴![]() ………………………………………………….8分
………………………………………………….8分
(3)假设存在![]() ,只需
,只需![]() ,就有
,就有![]() .
.
则![]()
![]()
![]() (x+t+1)2≤x
(x+t+1)2≤x![]() x2+(2t-2)x+t2+2t+1≤0…….10分
x2+(2t-2)x+t2+2t+1≤0…….10分
令g(x)=x2+(2t-2)x+t2+2t+1,g(x)≤0,x∈[1,m]
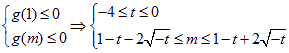 ………………………..12分
………………………..12分
∴m≤1-t+2![]() ≤1-(-4)+2
≤1-(-4)+2![]() =9
=9
即存在t=-4 ,对任意的x∈[1,9] 恒有g(x)≤0, ∴m的最大值为9……14分


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
| 2 |
| π |
| 6 |
| π |
| 4 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 2 |
| π |
| 6 |
| π |
| 4 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京大学附中高三(上)数学练习试卷5(文科)(解析版) 题型:填空题
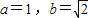 ,
,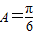 则
则 ;③设二次函数f(x)=x2+ax+a,则“
;③设二次函数f(x)=x2+ax+a,则“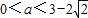 ”是“方程f(x)-x=0的两根x1和x2满足0<x1<x2<1”的充分必要条件.④过点(
”是“方程f(x)-x=0的两根x1和x2满足0<x1<x2<1”的充分必要条件.④过点( ,1)且与函数y=
,1)且与函数y=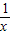 的图象相切的直线方程是4x+y-3=0.其中所有正确说法的序号是 .
的图象相切的直线方程是4x+y-3=0.其中所有正确说法的序号是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com