
����Ŀ������ƽ��ֱ������ϵxOy�У���֪����C1��x2+y2=1����ƽ��ֱ������ϵxOy��ԭ��OΪ���㣬x���������Ϊ���ᣬȡ��ͬ�ĵ�λ���Ƚ���������ϵ����ֱ֪��l���ѣ�2cos�ȩ�sin�ȣ�=6��
��1��������C1�ϵ����е�ĺ����ꡢ������ֱ��쳤Ϊԭ���� ![]() ��2����õ�����C2 �� ��д��ֱ��l��ֱ�����귽�̺�����C2�IJ������̣�
��2����õ�����C2 �� ��д��ֱ��l��ֱ�����귽�̺�����C2�IJ������̣�
��2��������C2����һ��P��ʹ��P��ֱ��l�ľ��������������ֵ��
���𰸡�
��1���⣺�������֪��ֱ��l��ֱ�����귽��Ϊ��2x��y��6=0��
��Ϊ����C2��ֱ�����귽��Ϊ�� ![]() ��
��
������C2�IJ��������� ![]() ����������
����������
��2���⣺��P�����꣨ ![]() �������P��ֱ��l�ľ���Ϊ��
�������P��ֱ��l�ľ���Ϊ��
![]() =
= ![]() ��
��
�൱sin��60�㩁�ȣ�=��1ʱ����P�� ![]() ����
����
��ʱ ![]()
����������1��ֱ��д��ֱ��l��ֱ�����귽�̣�������C1�ϵ����е�ĺ����ꡢ������ֱ��쳤Ϊԭ���� ![]() ��2����õ�����C2�ķ��̣�Ȼ��д������C2�IJ������̣���2���������C2��һ��P�����꣬���õ�P��ֱ��l�ľ��빫ʽ������������ʽ���������DZ任������ֵ��
��2����õ�����C2�ķ��̣�Ȼ��д������C2�IJ������̣���2���������C2��һ��P�����꣬���õ�P��ֱ��l�ľ��빫ʽ������������ʽ���������DZ任������ֵ��
�����㾫����ͨ��������õ㵽ֱ�ߵľ��빫ʽ�����յ�![]() ��ֱ��
��ֱ��![]() �ľ���Ϊ��
�ľ���Ϊ��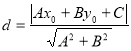 �����Խ����⣮
�����Խ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��Ŵ���ѧ�������������������������⣺�����������ף���֪������ǰ��ȡ�룬��������ȡһ�������ķ�ȡһ������һ���������ʣ����Σ�����ͼ�ǽ��������ij����ͼ��ִ�иó����ͼ���������S=1.5����λ��������������k��ֵΪ�� �� 
A.4.5
B.6
C.7.5
D.9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������
����p��x��0��x2��x+1��0����Vp��x0��0��x02��x0+1��0��
�����������ߵı���3��5��7��������ڽ�Ϊ ![]() �У�
�У�
���� ![]()
![]() =
= ![]()
![]() ����
���� ![]() =
= ![]() ��
��
��ac2��bc2��a��b�ij�ֲ���Ҫ������
����������ĸ���Ϊ�� ��
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() ��a��0����
��a��0����
��1��������y=f��x���ļ�ֵ��
��2����a��0����g��x��=x2emx �� �������x1 �� x2��[0��2]��f��x1����g��x2���ݩ�1���������m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڹ��Ϊ��ĵȲ�����{an}�У���֪a2=3����a1��a3��a7�ɵȱ����У�
��1��������{an}��ͨ�ʽ��
��2��������{an}��ǰn���ΪSn �� ��bn= ![]() ��������{bn}��ǰn���Tn ��
��������{bn}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������f��x��=2sin��2x+ ![]() ����ͼ������ƽ�Ʀգ��գ�0������λ���ٽ�ͼ����ÿһ��ĺ��������̵�ԭ����
����ͼ������ƽ�Ʀգ��գ�0������λ���ٽ�ͼ����ÿһ��ĺ��������̵�ԭ���� ![]() ���������겻�䣩������ͼ�����ֱ��x=
���������겻�䣩������ͼ�����ֱ��x= ![]() �Գƣ���յ���СֵΪ�� ��
�Գƣ���յ���СֵΪ�� ��
A.![]() ��
��
B.![]() ��
��
C.![]() ��
��
D.![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڼ�����ϵ�£���֪ԲO����=cos��+sin�Ⱥ�ֱ��l����sin���ȩ� ![]() ��=
��= ![]() ��
��
��1����ԲO��ֱ��l��ֱ�����귽�̣�
��2�����ȡʣ�0���У�ʱ����ֱ��l��ԲO������ļ����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=Asin����x+�գ���x��R������A��0���أ�0�� ![]() �����䲿��ͼ����ͼ��ʾ�� ��I����f��x���Ľ���ʽ��
�����䲿��ͼ����ͼ��ʾ�� ��I����f��x���Ľ���ʽ��
��II������ ![]() ������
������ ![]() �ϵ����ֵ����Ӧ��xֵ��
�ϵ����ֵ����Ӧ��xֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com