|
|
|
如图,△ABC是直角三角形,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=2BC=4,EA=3,FC=1.
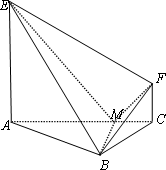
(1)证明:EM⊥BF;
(2)求平面BEF与平面ABC所成的锐二面角的余弦值.
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
在△ABC中,角A,B,C的对边分别为a,b,c且a+c=10,C=2A,cosA= . .
求:(Ⅰ) 的值; 的值;
(Ⅱ)b的值.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若x,y满足条件 ,则目标函数z=x+2y+1的最大值是________. ,则目标函数z=x+2y+1的最大值是________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知函数f(x)=x2-5x+4,则不等式组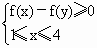 表示的平面区域为 表示的平面区域为
|
| [ ] |
A. |
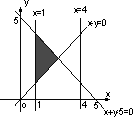
|
B. |
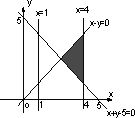
|
C. |
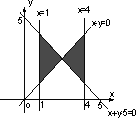
|
D. |
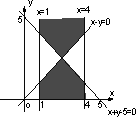
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
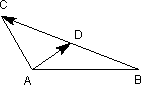
如下图,在△ABC中,AB=3,AC=2,D是边BC的中点,则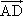 · ·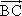 =________. =________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若集合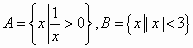 ,则A∩B= ,则A∩B=
|
| [ ] |
A. |
{x|x<0}
|
B. |
{x|0<x<3}
|
C. |
{x|x>4}
|
D. |
R
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
某车间分批生产某种产品,每批的生产准备费用为800元.若每批生产x件,则平均仓储时间为 ,且每件产品每天的仓储费用为1元.为使平均到每件产品的生产准备费用 ,且每件产品每天的仓储费用为1元.为使平均到每件产品的生产准备费用
与仓储费用之和最小,每批应生产产品
|
| [ ] |
A. |
60件
|
B. |
80件
|
C. |
100件
|
D. |
120件
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
将函数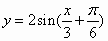 的图象按向量a=( 的图象按向量a=( ,2)平移后所得图象的函数为 ,2)平移后所得图象的函数为
|
| [ ] |
A. |

|
B. |

|
C. |

|
D. |

|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合.已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x+mn=0的两个根.

(Ⅰ)证明:C,B,D,E四点共圆;
(Ⅱ)若∠A=90°,且m=4,n=6求C,B,D,E所在圆的半径.
|
|
|
查看答案和解析>>
